Ableitung einer nicht entwickelten Funktion
1. Wie differenziert man eine implizite Funktion?
Lösung:
Sei eine implizite Funktion F[x; f(x)] = 0 gegeben. Beim Differenzieren differenziert man die Terme, die nur x enthalten, auf die übliche Weise; die Terme mit y werden als zusammengesetzte Funktionen differenziert. Man multipliziert ihre Ableitung (nach y) mit y′. Dann löst man die Gleichung nach y′ auf.
Zum Beispiel:
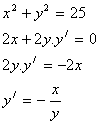
2. Differenziere die Funktion:
Lösung:
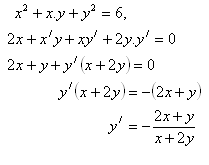
3. Differenziere die Funktion:
Lösung:
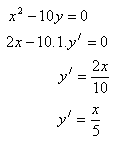
4. Differenziere die Funktion:
Lösung:
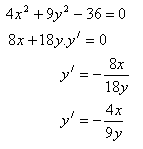
5. Unter welchem Winkel schneiden sich die Kurven x2 + y2 – 5 = 0 und y2 – 4x = 0?
Lösung:
Der Winkel zweier sich schneidender Kurven entspricht dem Winkel ihrer Tangenten im gemeinsamen Punkt T. Gemeinsamer Punkt T:
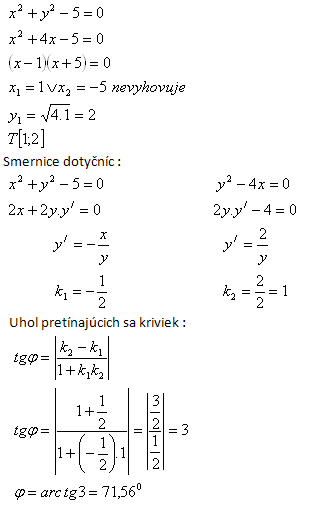
6. Differenziere die Funktion x3 + y3 − 3axy = 0
Lösung:
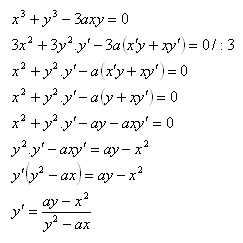
7. Differenziere die Funktion ey + e–x + xy = 0
Lösung:
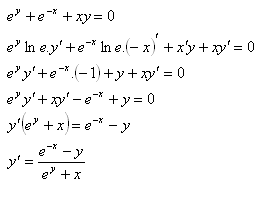
8. Berechne die erste Ableitung der Funktion exy − x2 + y3 = 0 für x = 0
Lösung:
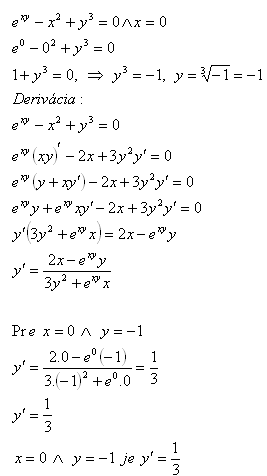
9. Schreibe die Gleichung der Tangente an den Kreis x2 + y2 + 4x − 4y + 3 = 0 an dem Punkt, an dem der Kreis die x-Achse schneidet.
Lösung:
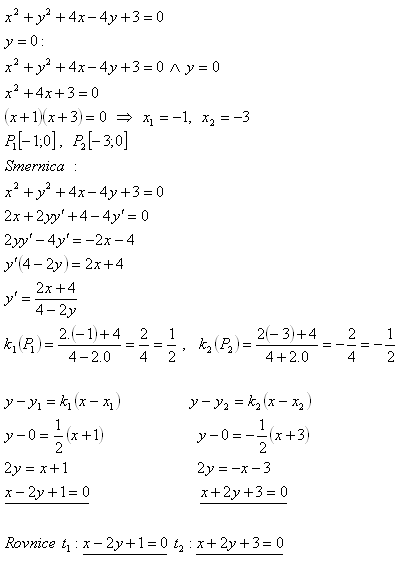
10. Schreibe die Gleichung der Tangente an die Kurve
Lösung:
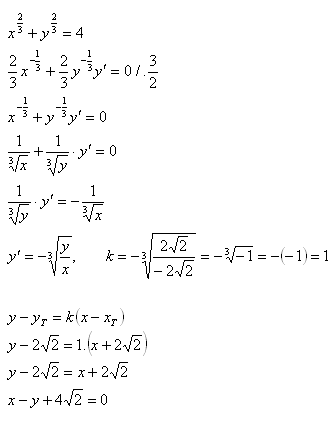
Die Gleichung der Tangente ist x − y + 4√2 = 0