Extreme – praktische Probleme
1.Teile die Zahl 32 in zwei Summanden, so dass ihr Produkt maximal ist.
Lösung:
Erster Summand: x x = 16
Zweiter Summand: 32 – x 32 – 16 = 16
y = x.(32 – x)
y = 32x – x2
y‘ = 32 – 2x
32 – 2x = 0
2x = 32
x =16
y‘‘ = -2 < 0 - Maximum
Der erste Summand ist 16, der zweite ist ebenfalls 16.
2.Teile die Zahl 16 in zwei Summanden, so dass die Summe der Quadrate dieser Summanden minimal ist.
Lösung:
Erster Summand: x x = 8
Zweiter Summand: 16 – x 16 – 8 = 8
y = x2 + ( 16 – x )2
y = x2 + 256 -32x +x2
y = 2x2 – 32x + 256
y‘ = 4x – 32
4x - 32 = 0
4x = 32
x = 8
y‘‘ = 4 > 0 - Minimum
Der erste Summand ist 8, der zweite ist ebenfalls 8.
3.Finde eine positive Zahl x, so dass die Summe dieser Zahl und ihres Kehrwerts minimal ist.
Lösung:
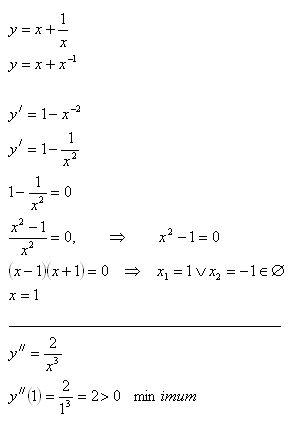
Die gesuchte Zahl ist x = 1.
4.Aus einem Draht der Länge l = 120 cm soll ein Modell eines Quaders mit quadratischer Grundfläche hergestellt werden. Welche Abmessungen soll er haben, damit seine Oberfläche maximal ist?
Lösung:
Kanten der quadratischen Grundfläche: a = b = x
Höhe des Quaders: c
8x + 4c = l
8x +4c =120/:4
2x + c = 30
c = 30 – 2x
S = 2( ab + ac + bc )
S = 2( x.x + x(30 – 2x) + x(30 – 2x))
S = 2(-3x2 +60x )
S = -6x2 +120x
S‘ = -12x + 120 S‘‘ = -12 < 0 Maximum
-12x + 120 = 0
12x = 120
x = 10
c = 30 -2x = 30 – 2·10 = 10
x = 10 cm, c = 10 cm .
Der Quader muss ein Würfel mit Kantenlänge x = 10 cm sein.
5.Ein rechteckiger Garten hat den Umfang 200 m. Bestimme die Abmessungen des Gartens, so dass seine Fläche maximal ist.
Lösung:
a = x
P = 2a + 2b
200 = 2x +2b/:2
100 = x + b
b = 100 – x b = 100 – x = 100 – 50 = 50
b = 50 m
S = a.b
S = x.(100 – x )
S = 100x – x2
S‘ =100 – 2x S‘‘ = -2 < 0 - Maximum
100 – 2x = 0
2x = 100
x = 50
a = 50 m
Der Garten hat die größte Fläche, wenn er ein Quadrat mit Seiten a = b = 50 m ist.
6.Wann hat ein Quader mit Volumen V = 63 cm3 und Höhe v = 7 cm die kleinste Oberfläche?
Lösung:
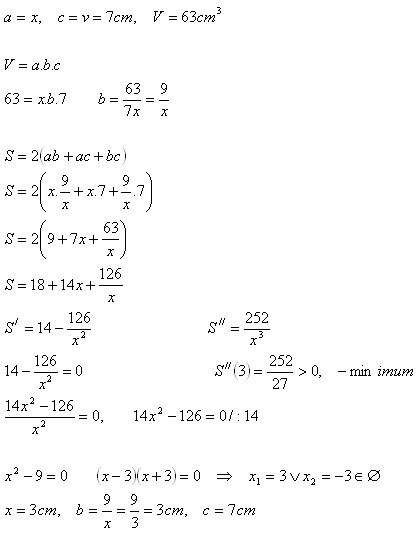
Die Abmessungen des gesuchten Quaders sind a = 3 cm, b = 3 cm, c = 7 cm.
7.Am Flussufer soll ein rechteckiger Garten (eine Seite des Rechtecks wird vom Fluss gebildet) mit Draht der Länge l = 800 m eingezäunt werden. Welche Abmessungen muss der Garten haben, damit seine Fläche maximal ist?
Lösung:
800 = 2a + b
a = x
b = 800 – 2a = 800 – 2x
S = a.b
S = x.(800 – 2x)
S = 800x – 2x2
S‘ =800 – 4x S‘‘ = -4 < 0 - Maximum
800 – 4x = 0
4x = 800
x = 200
x = 200 m
b = 800 – 2x
b = 800 – 400 = 400
b = 400 m
Die Abmessungen des Gartens sind a = 200 m, b = 400 m.
8.Welche Abmessungen hat ein offenes Becken mit quadratischer Grundfläche, wenn das Volumen des Beckens V = 32 m3 ist und die Materialmenge für seinen Bau minimal sein soll?
Lösung:
V = 32 m3, x – Kante der quadratischen Grundfläche, v – Höhe des Quaders
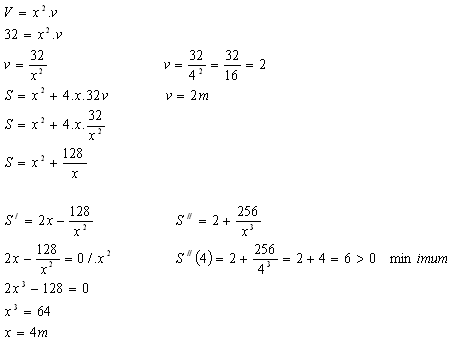
Abmessungen: a = 4 m, b = 4 m, v = 2 m
9.Ein Draht der Länge 5 m wird so rechtwinklig gebogen, dass der Abstand seiner beiden Enden minimal ist. Wo soll der Draht gebogen werden?
Lösung:
Schenkel a = x, b = 5 – x
Hypotenuse c = y
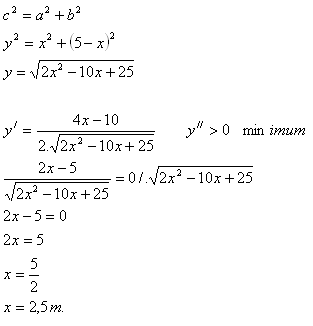
Der Draht soll in der Mitte gebogen werden.
10.Aus einem quadratischen Blech mit Seitenlänge 30 cm sollen in den Ecken vier gleich große Quadrate ausgeschnitten werden, und der Rest wird zu einer offenen Schachtel gefaltet. Bestimme die Seitenlänge x der ausgeschnittenen Quadrate, so dass das Volumen der Schachtel maximal ist.
Lösung:
a = 30 – 2x, b = 30 – 2x, c = x
V = a·b·c
V = (30 – 2x)(30 – 2x)·x
V = 4x3 – 120x2 +900x
V‘ = 12x2 – 240x +900 V‘‘ = 24x -240
12x2 – 240x +900 =0 /:12 V‘‘(5) = 24·5 -240 = -120 < 0 Maximum
x2 - 20x + 75 = 0
( x – 5 )( x -15 ) = 0 x1 = 5 x2 = 15 - nicht zulässig
x = 5 cm
Die Seitenlänge des ausgeschnittenen Quadrats ist x = 5 cm.
11.Eine Grube mit Volumen 500 m3 hat die Form eines Quaders mit quadratischer Grundfläche der Seitenlänge x und Tiefe h. Für welche Abmessungen x und h hat die Grube die kleinste Oberfläche?
Lösung:
Analyse:
V = 500 m3, x = ?, h = ?
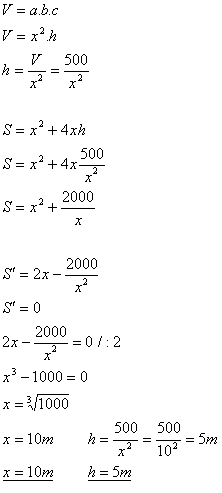
Die Grube hat eine quadratische Grundfläche mit Seitenlänge x = 10 m und Höhe h = 5 m.
12.Gegeben ist die Parabel y = 4 – x2. Finde die Eckpunkte des Rechtecks ABCD mit größtem Umfang, dessen Eckpunkte A, B auf der x-Achse liegen und dessen Eckpunkte C, D positive y-Koordinaten haben und auf der Parabel liegen.
Lösung:
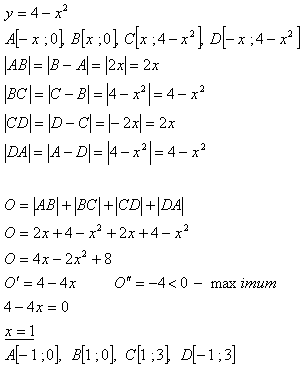
Die Punkte sind: A[-1;0], B[1;0], C[1;3], D[-1;3]
13.Bestimme die Abmessungen (r, v) eines zylindrischen Gefäßes ohne Deckel mit Oberfläche S = 27π so, dass sein Volumen maximal ist.
Lösung:
Analyse:
S = 27π, r = x
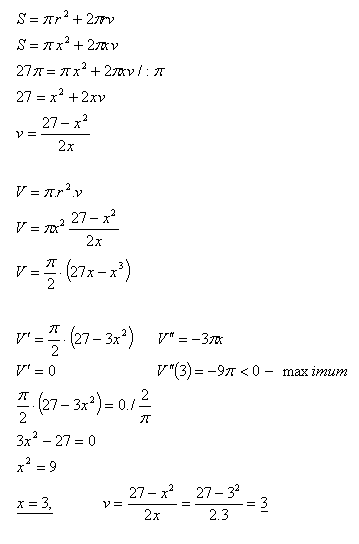
Die Abmessungen des Gefäßes sind r = x = 3 cm, v = 3 cm.
14.Ein zylindrischer Behälter ohne Deckel hat das Volumen V = 3140 cm3. Bestimme die Zylinderabmessungen (r, v), so dass für seine Herstellung die geringstmögliche Materialmenge benötigt wird.
Lösung:
Analyse:
V = 3140 cm3, r = x = ?
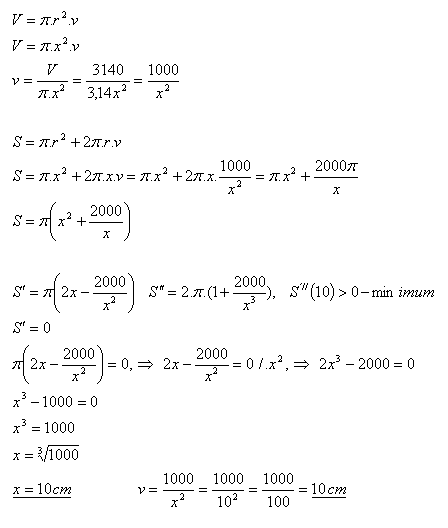
Die Abmessungen des Gefäßes sind r = x = 10 cm, v = 10 cm.
15.Welche Abmessungen muss ein Rechteck mit Umfang P = 40 cm haben, damit seine Diagonale minimal ist?
Lösung:
Analyse:
x = a = ?, b = ?
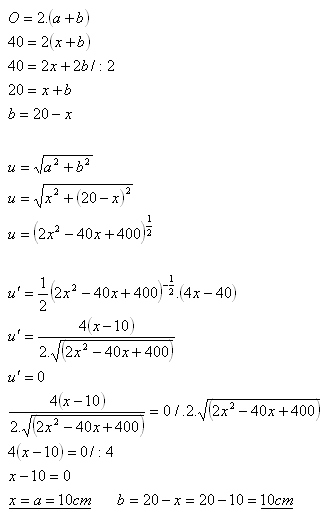
Die Figur ist ein Quadrat mit Seitenlänge a = 10 cm.