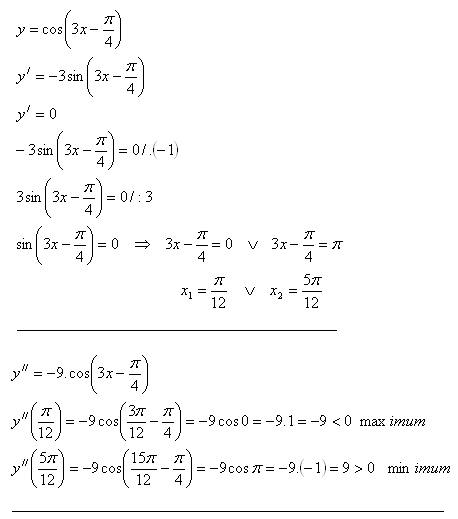Verhalten einer Funktion

1. Wie bestimmen wir das Verhalten einer Funktion?

Lösung:

a.) Die Funktion y = f(x) ist an der Stelle x₀ wachsend, wenn f‘(x₀) > 0

b.) Die Funktion y = f(x) ist an der Stelle x₀ fallend, wenn f‘(x₀) < 0

c.) Die Funktion y = f(x) hat an der Stelle x₀ einen stationären Punkt, wenn f‘(x₀) = 0

d.) Die Funktion y = f(x) ist an der Stelle x₀ konvex, wenn f‘‘(x₀) > 0

e.) Die Funktion y = f(x) ist an der Stelle x₀ konkav, wenn f‘‘(x₀) < 0

f.) Die Funktion y = f(x) hat an der Stelle x₀ einen Wendepunkt, wenn f‘‘(x₀) = 0 ^ f‘‘(x₀) ≠ 0

g.) Die Funktion y = f(x) hat an der Stelle x₀ ein lokales Minimum, wenn f‘ (x₀) = 0 ^ f‘‘ (x₀) > 0

h.) Die Funktion y = f(x) hat an der Stelle x₀ ein lokales Maximum, wenn f‘ (x₀) = 0 ^ f‘‘ (x₀) < 0

2. Gegeben ist die Funktion y = x³ – 5x² + 3x - 5. Bestimmen Sie für welche x die Funktion wachsend, fallend, konvex und konkav ist.

Lösung:

Stationäre Punkte:
$y = x^3 - 5x^2 + 3x - 5$
$y^{'} = 3 x^{2} - 10 x + 3$
$3x^2 - 10x + 3 = 0$

$3(x - 3)\left(x - \frac{1}{3}\right) = 0$
$x_{1} = 3$ oder $x_2 = \frac{1}{3}$

Wachsende Funktion:

$3 (x - 3) (x - \frac{1}{3}) > 0$

Division durch 3:
$(x - 3) (x - \frac{1}{3}) > 0$

Mit Hilfe der Vorzeichenanalyse des quadratischen Ausdrucks:

[x - 3 > 0 \;\wedge\; x - \tfrac{1}{3} > 0] \quad \lor \quad [x - 3 < 0 \;\wedge\; x - \tfrac{1}{3} < 0]

[x > 3 \;\wedge\; x > \tfrac{1}{3}] \quad \lor \quad [x < 3 \;\wedge\; x < \tfrac{1}{3}]

Also:
$x > 3$ oder $x < \frac{1}{3}$

x \in (-\infty, \tfrac{1}{3}) \cup (3, +\infty)

Fallende Funktion:

x \in \mathbb{R} - \left( (-\infty, \tfrac{1}{3}) \cup (3, +\infty) \right) = \left( \tfrac{1}{3}, 3 \right)

Wendepunkt:

$y'' = 6x - 10$

$6x - 10 = 0$

x_{\text{inf}} = \frac{5}{3}

Konvexe Funktion:

$6 x - 10 > 0$

x > \frac{5}{3}

x \in \left(\tfrac{5}{3}, +\infty\right)

Konkave Funktion:

$6 x - 10 < 0$

x < \frac{5}{3}

x \in (-\infty, \tfrac{5}{3})

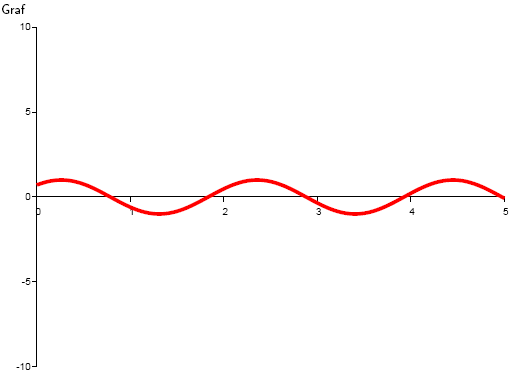
Graph

function-behavior-2a-g

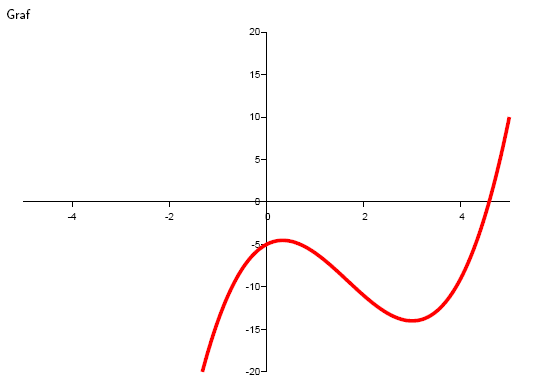
3.Überprüfen Sie, ob die Funktion y = x³ -5x² +3x -5 an der Stelle x₀ = 2 fallend und konvex ist.

Lösung:

y = x³ -5x² +3x -5

y‘ = 3x² -10x +3

y‘(2) = 3·2² -10·2 +3

y‘(2) = -5 < 0

Die Funktion ist fallend.

y‘ = 3x² -10x +3

y‘‘ = 6x - 10

y‘‘(2) = 6·2 – 10

y‘‘(2) = 2 > 0

Die Funktion ist konvex.

graph

4.Überprüfen Sie, ob die Funktion in einer Umgebung von x₀ = 0 wachsend und konkav ist.

Lösung:

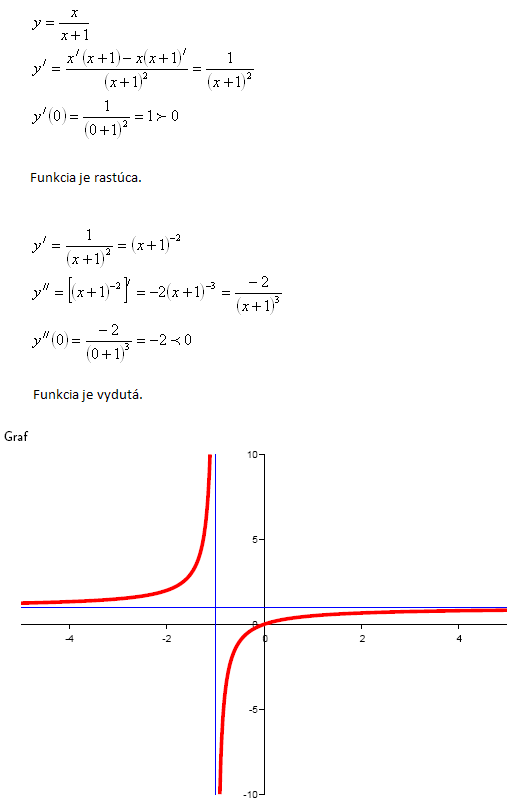
function-behavior-4a

Die Funktion ist wachsend und konvex.

5. Gegeben ist die Funktion y = 2x² – ln x. Bestimmen Sie für welche x die Funktion fallend ist.

Lösung:

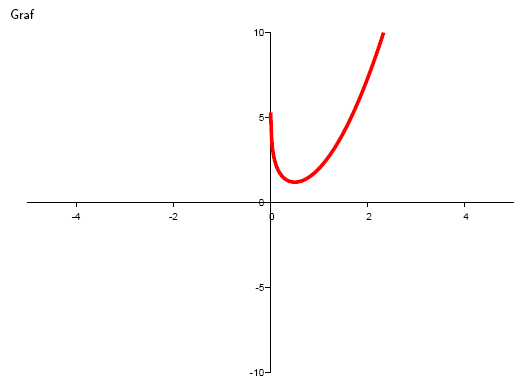
function-behavior-5g

Die Funktion ist fallend.

6. Bestimmen Sie die lokalen Extrema der Funktion y = x²(4 – x )²

Lösung:

Lokale Extrema:

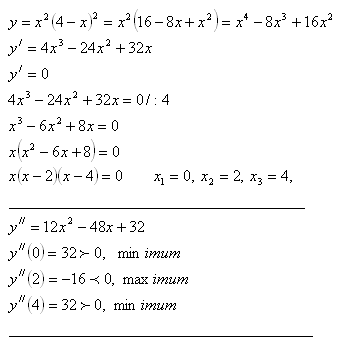
function-behavior-6

Die Funktion hat ein lokales Minimum bei x₁ = 0 und x₃ = 4 und ein lokales Maximum bei x₂ = 2.

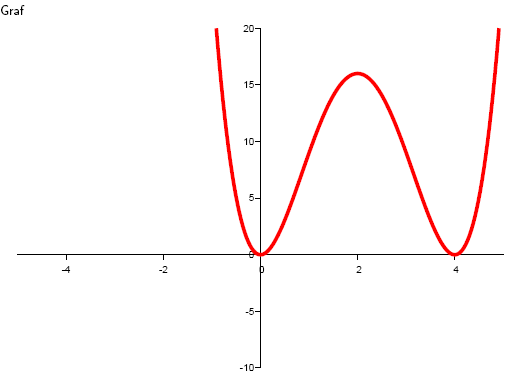
function-behavior-6g

7. Bestimmen Sie die lokalen Extrema der Funktion y = sin x · (1+cos x)

Lösung:

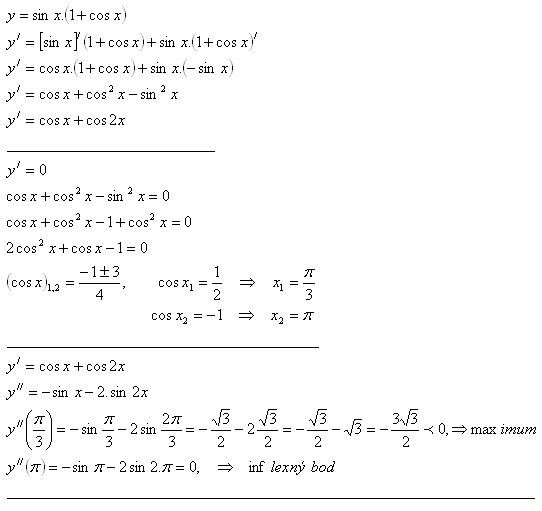
function-behavior-7a

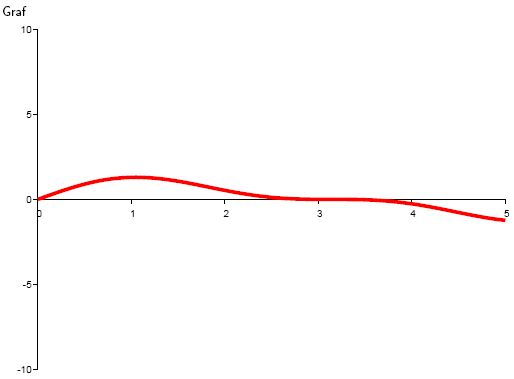
function-behavior-7g

8.Bestimmen Sie die stationären Punkte und die Intervalle des Wachsens und Fallens der Funktion

Lösung:

Stationäre Punkte: Wachsen oder Fallen der Funktion:

function-behavior-8a

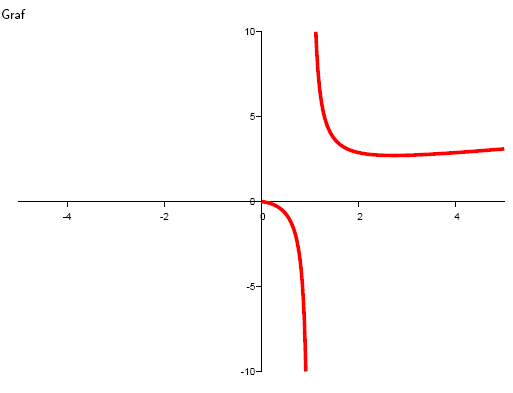
function-behavior-8g

Die Funktion hat einen stationären Punkt $S(e$ . Sie ist wachsend für $x \in (e, +\infty)$ und fallend für $x \in ($ $-\infty$ $x \in (0, e)$ .

9.Für welche Werte von a, b ist der Punkt I[1; 3] ein Wendepunkt der Funktion y = ax³ + bx² ?

Lösung:

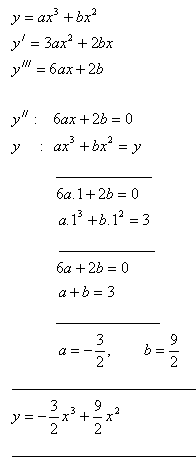
function-behavior-9

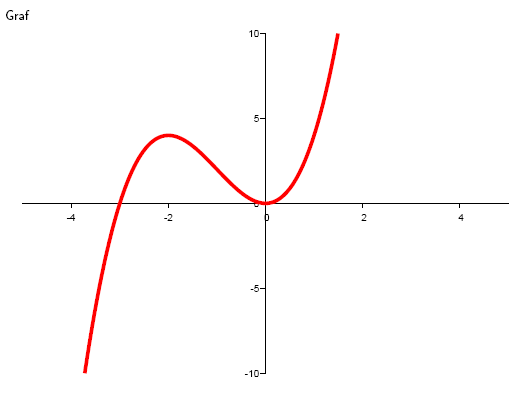
function-behavior-9g

10. Bestimmen Sie die lokalen Extrema der Funktion

Lösung:

function-behavior-10a

function-behavior-10g

Mathematik

Verhalten einer Funktion

Adblock detected