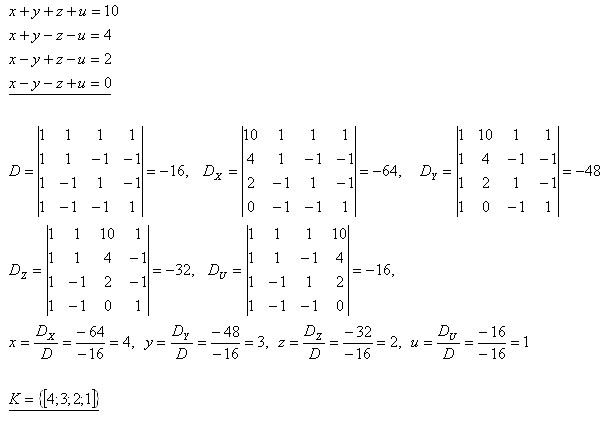Determinante

1. Was ist eine Determinante und welche Eigenschaften hat sie?

Lösung:

Die Determinante n-ter Ordnung ist eine Zahl D, gebildet aus n² Zahlen a_ik, die in einer quadratischen Tabelle mit n Zeilen und n Spalten der Form angeordnet sind:

a₁₁,a₁₂,...a_1n => Zeile der Determinante

a₁₁,a₂₁,...a_n1 => Spalte der Determinante

a₁₁,a₂₂,...a_nn => Hauptdiagonale

Wert der Determinante:

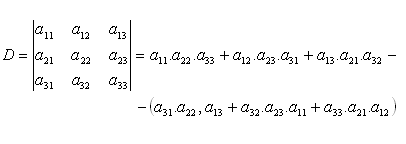
Determinante 2. Ordnung

Determinante 3. Ordnung (Regel von Sarrus)

Determinante n-ter Ordnung:

Eine Determinante n-ter Ordnung hat n Zeilen und n Spalten (n > 3). Die zu dem Element a_ij gehörende Untermatrix (Minor) M_ij erhält man aus der Determinante D durch Streichen der i-ten Zeile und der j-ten Spalte.

Algebraisches Komplement (Kofaktor):

A_ij = (-1)^i+j · a_ij · M_ij

Entwicklung einer Determinante:

a.) nach der i-ten Zeile:

D = a_i1M_i1 + a_i2M_i2 + ... + a_inM_in

b.) nach der j-ten Spalte:

D = a_1jM_1j + a_2jM_2j + ... + a_njM_nj

2. Formuliere die Sätze über den Wert einer Determinante.

Lösung:

1) Der Wert der Determinante ändert sich nicht, wenn wir ihre Zeilen mit ihren Spalten vertauschen (d. h. transponieren).
2) Der Wert der Determinante ändert sich nicht, wenn wir zu einer Zeile ein Vielfaches einer anderen Zeile addieren (oder davon subtrahieren).
3) Der Wert der Determinante ist Null, wenn alle Elemente einer Zeile Null sind.
4) Der Wert der Determinante ist Null, wenn eine Zeile ein skalares Vielfaches einer anderen Zeile ist.
5) Der Wert der Determinante ist Null, wenn zwei Zeilen identisch sind.
6) Die Determinante ändert ihr Vorzeichen, wenn wir zwei Zeilen der Determinante vertauschen.
7) Man kann eine Zahl „c“ aus der Determinante ausklammern, die eine Zeile multipliziert.
8) Die Multiplikation der Determinante mit einer Zahl „c“ entspricht der Multiplikation einer ihrer Zeilen mit dieser Zahl (nur einer einzigen Zeile). c <> 0

Hinweis:

Die genannten Eigenschaften gelten ebenso für die Spalten der Determinante.

3. Berechne die Determinanten:

Lösung:

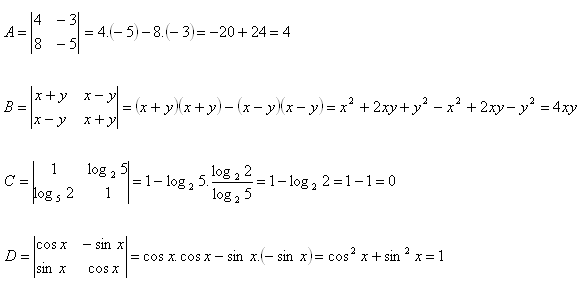
4. Berechne die Determinanten:

Lösung:

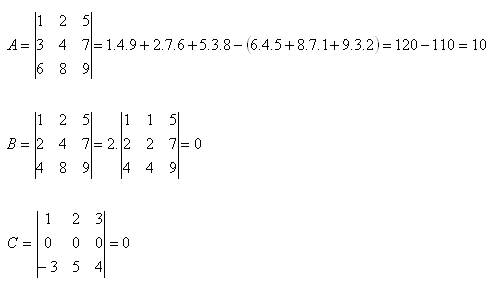
5. Berechne die Determinanten:

Lösung:

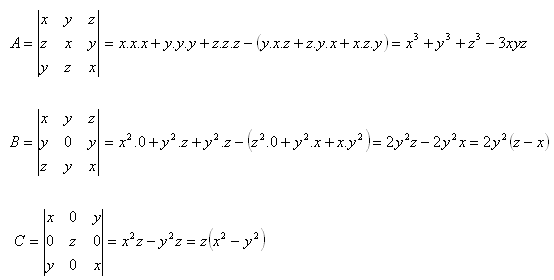
6. Löse die Gleichungen in R:

Lösung:

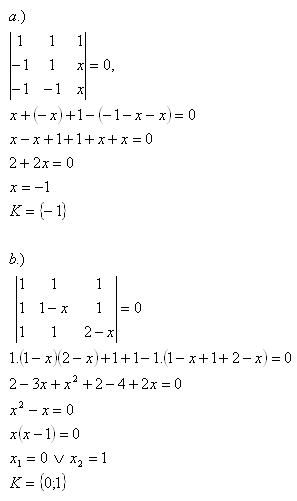
7. Löse die Gleichungen in R:

Lösung:

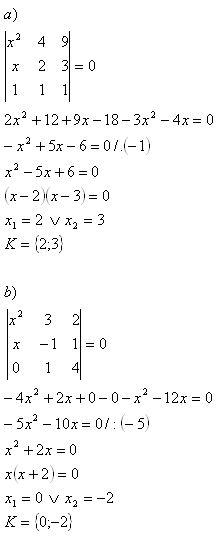
8. Berechne den Flächeninhalt des Dreiecks ABC mit den Eckpunkten:

A[3;2], B[6;3], C[4;7]

Lösung:

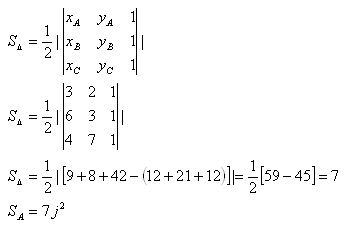
Der Flächeninhalt des Dreiecks ABC ist 7 j²

9. Berechne den Flächeninhalt des Dreiecks ABC, dessen Seiten die Gleichungen haben:

Lösung:

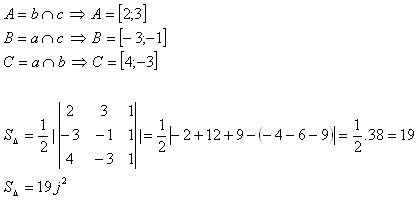
Der Flächeninhalt des Dreiecks ABC ist 19 j²

10. Bestimme, ob die Punkte A, B, C auf einer Geraden liegen, wenn:

A[1;4], B[3;0], C[0;6]

Lösung:

Die Bedingung dafür, dass die Punkte A[x_a;y_a], B[x_b;y_b], C[x_c;y_c] auf einer Geraden liegen, ist

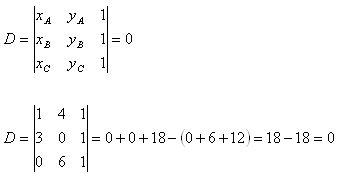
D = 0 => Die Punkte A, B, C liegen auf derselben Geraden

11. Bestimme, ob die Punkte A, B, C auf einer Geraden liegen, wenn:

A[1;1], B[0;4], C[4;3]

Lösung:

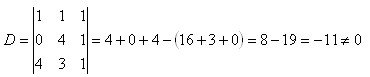
D <> 0 => Die Punkte liegen nicht auf derselben Geraden

12. Gegeben sind die Punkte A, B, C. Bestimme die erste Koordinate des Punktes B so, dass A, B, C auf einer Geraden liegen. Gegeben:

A[0;3], B[x_B;-1], C[-3;9]

Lösung:

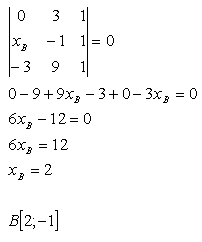
13. Schreibe die Gleichung der Geraden, die durch die Punkte A und B verläuft, wenn:

A[3;2], B[0;4]

Lösung:

Liegen die Punkte A[x_a;y_a], B[x_b;y_b], X[x,y] auf der Geraden p, dann gilt

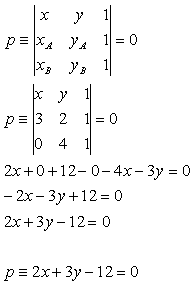
14. Schreibe die Gleichungen der Seiten des Dreiecks ABC mit den Eckpunkten

A[4;2], B[7;3], C[1;6]

Lösung:

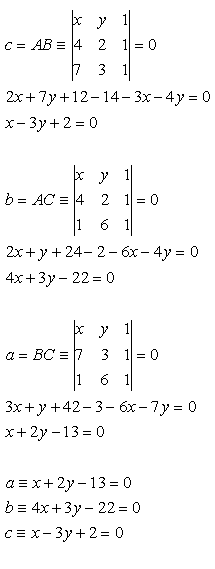
15. Berechne das Vektorprodukt (Kreuzprodukt) zweier Vektoren:

Lösung:

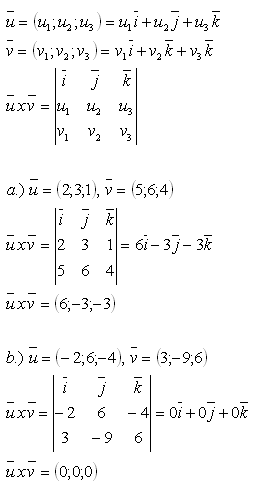
16. Löse die linearen Gleichungssysteme:

Lösung:

Cramersche Regel 1.

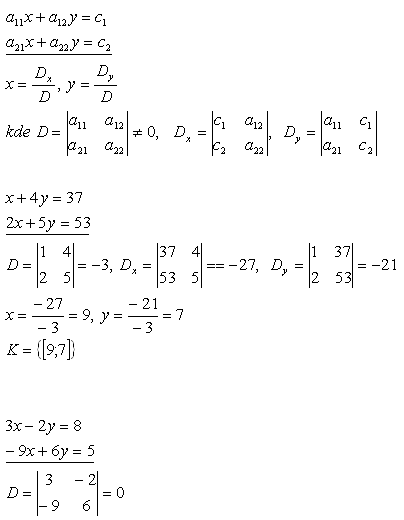
Das System hat keine Lösung

17. Löse das lineare Gleichungssystem:

Lösung:

Cramersche Regel 2.

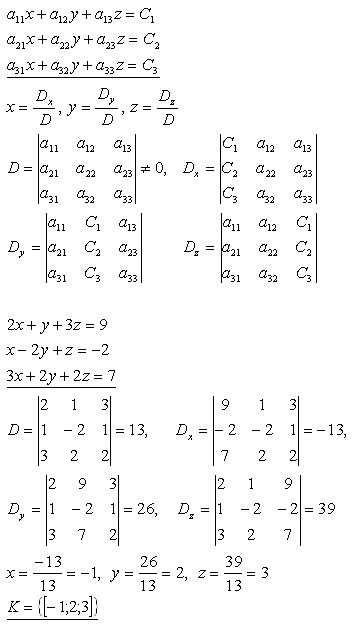
determinant-17r

18. Löse das lineare Gleichungssystem:

Lösung:

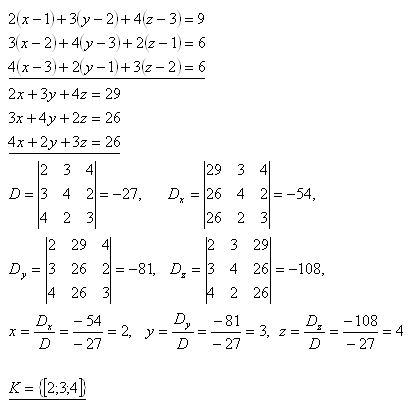
determinant-18r

19. Bestimme für die gegebene Determinante D das algebraische Komplement A₂₃

Lösung:

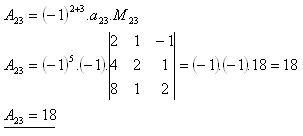
determinant-19r

20. Berechne die Determinante:

Lösung:

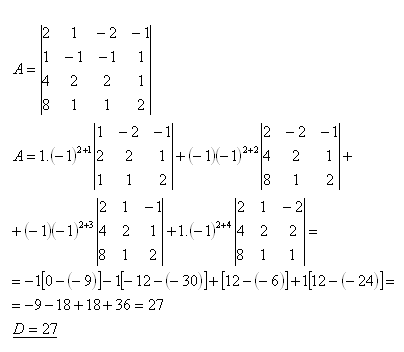
determinant-20r

21. Berechne die Determinante:

Lösung:

Entwicklung nach der vierten Zeile:

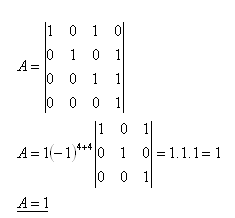
determinant-21r

22. Bestimme, ob die Punkte A, B, C, D in derselben Ebene liegen, wenn:

A[2;2;-2], B[1;1;4], C[0;2;0], D[3;1;2]

Lösung:

Bedingung:

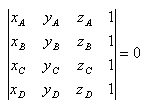
determinant-22ra

Lösung:

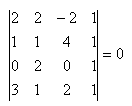
determinant-22rb

Entwicklung nach der dritten Zeile:

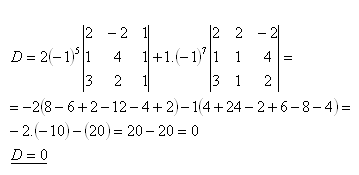
determinant-22rc

Die Punkte A, B, C, D liegen in derselben Ebene.

23. Schreibe die allgemeine Gleichung der Ebene, die durch die Punkte A, B, C gegeben ist, wenn:

A[0;0;5], B[-2;0;1], C[1;2;4]

Lösung:

Gleichung der Ebene:

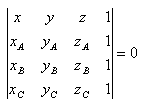
determinant-23ra

Lösung:

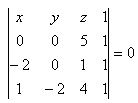
determinant-23rb

Entwicklung nach der zweiten Zeile:

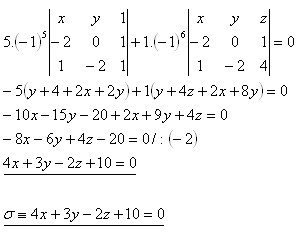
determinant-23rc

24. Schreibe die allgemeine Gleichung der Ebene, die durch die Punkte A, B, C verläuft, wenn

A[2;1;2], B[1;-2;3], C[0;0;0]

Lösung:

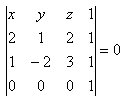
determinant-24ra

Entwicklung nach der vierten Zeile:

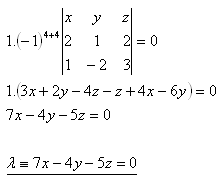
determinant-24rb

25. Löse das Gleichungssystem:

x + y + z + u = 10

x + y – z – u = 4

x – y + z – u = 2

x – y – z + u = 0

Lösung:

Mathematik

Determinante

Adblock detected