Matrix
1. Was sind die grundlegenden Eigenschaften von Matrizen.
Lösung:
Ein rechteckiges Schema aus m, n reellen Zahlen, angeordnet in m Zeilen und n Spalten, heißt Matrix (vom Typ m,n). Wenn m = n ist, handelt es sich um eine quadratische Matrix vom Grad n. Die Zahlen a11, a32, ... amn werden Elemente der Matrix genannt.
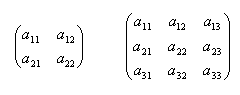
Nullmatrix: Einheitsmatrix:
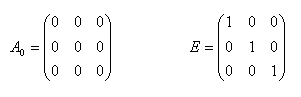
Inverse Matrix A–1:
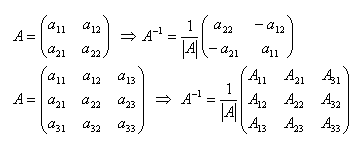
Summe der Matrizen A + B
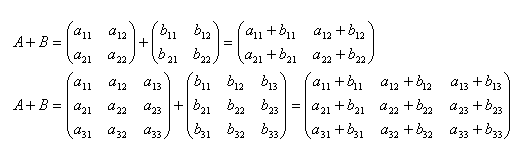
2. Erklären Sie das Verfahren zur Multiplikation zweier Matrizen.
Lösung:
Das Produkt zweier Matrizen ist nur dann definiert, wenn die linke Matrix genauso viele Spalten hat, wie die rechte Matrix Zeilen hat. Solche Matrizen nennt man „konform“.
Das Produkt von Matrizen ist nicht kommutativ!
Multiplikation einer Matrix mit einer Zahl:
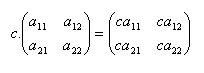
Produkt der Matrizen A·B
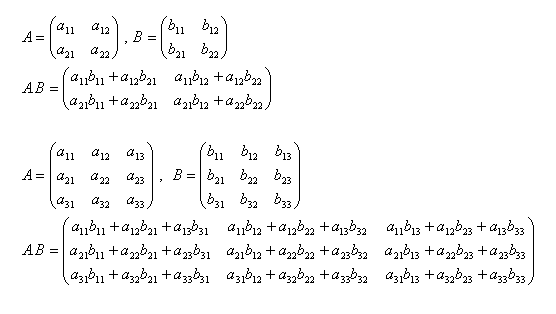
3.Addieren Sie die Matrizen A+B und M+N, wenn
Lösung:
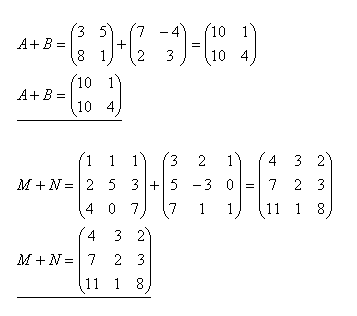
4.Multiplizieren Sie die Matrizen A·B und C·D, wenn
Lösung:
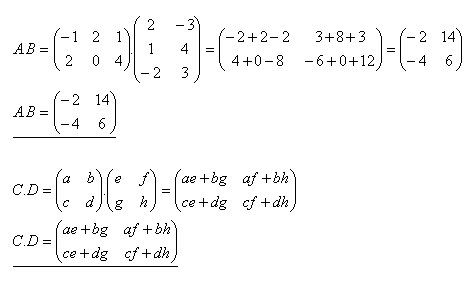
5.Zeigen Sie, dass das Produkt von Matrizen nicht kommutativ ist.
Lösung:
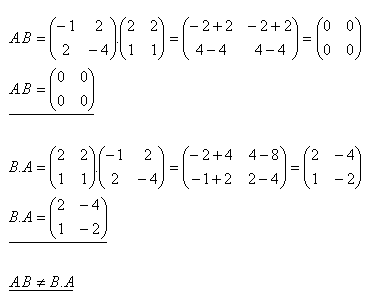
6.Gegeben ist die Matrix A. Bestimmen Sie die Matrix A2, wenn
Lösung:
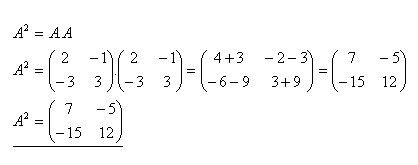
7.Gegeben ist die Matrix B. Bestimmen Sie die Matrix B2, wenn
Lösung:
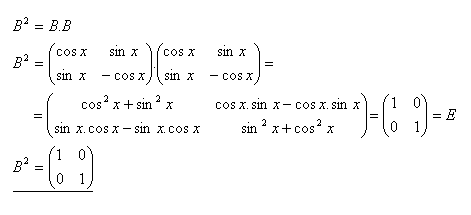
8.Berechnen Sie das Produkt der Matrizen A·B, wenn
Lösung:
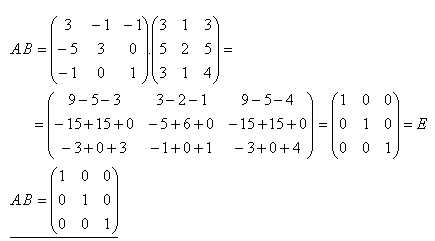
9.Erklären Sie das Verfahren zur Berechnung der inversen Matrix A–1 aus Matrix A.
Lösung:
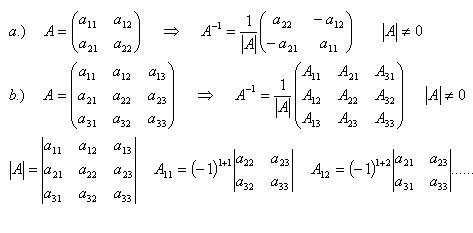
Bei der Kontrolle muss die inverse Matrix von links multipliziert werden.
Für das Produkt von Matrizen gilt das Kommutativgesetz nicht.
10.Bestimmen Sie für die Matrix A die inverse Matrix A–1 und überprüfen Sie, ob
Lösung:
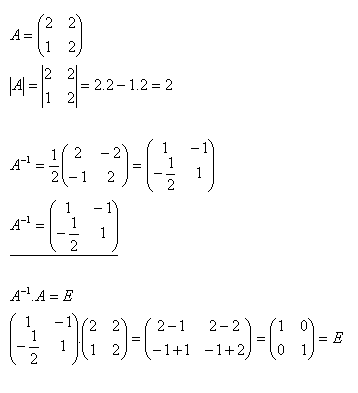
11.Bestimmen Sie für die Matrix A die inverse Matrix A–1 und überprüfen Sie, ob
Lösung:
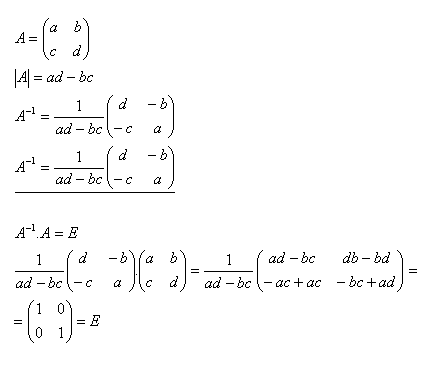
12.Berechnen Sie die inverse Matrix A–1 für die Matrix A, wenn
Lösung:
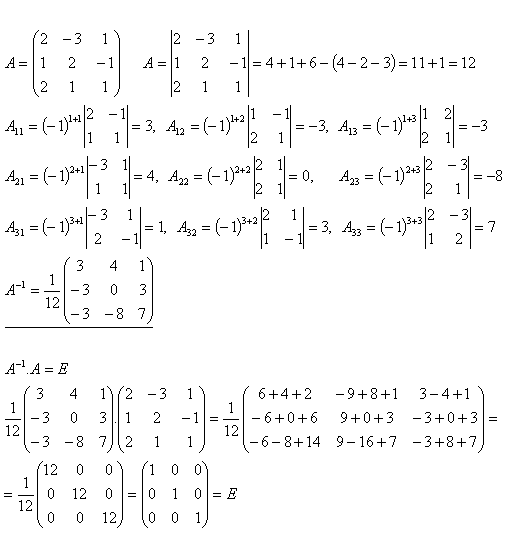
13.Berechnen Sie die inverse Matrix A–1 für die Matrix A und überprüfen Sie (siehe Beispiel 12), wenn
Lösung:
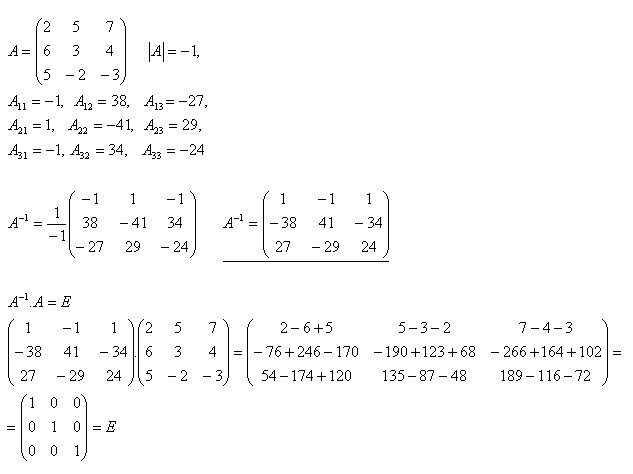
14.Lösen Sie die Matrixgleichung A + X = B, wenn
Lösung:
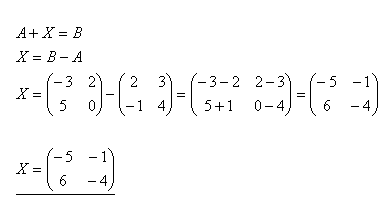
15.Berechnen Sie die Matrix X aus der Gleichung 2A + 3X = B, wenn
Lösung:
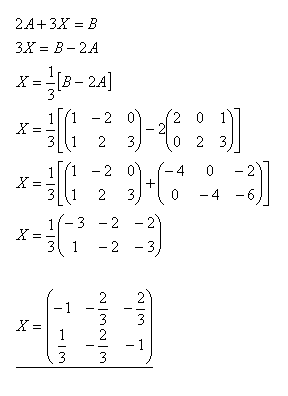
16.Lösen Sie die Matrixgleichung A·X = B und überprüfen Sie, ob
Lösung:
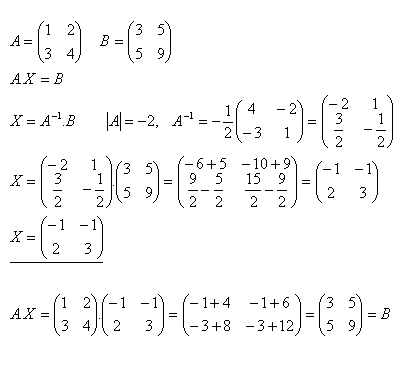
17.Lösen Sie die Gleichung A·X = B und überprüfen Sie, ob
Lösung:
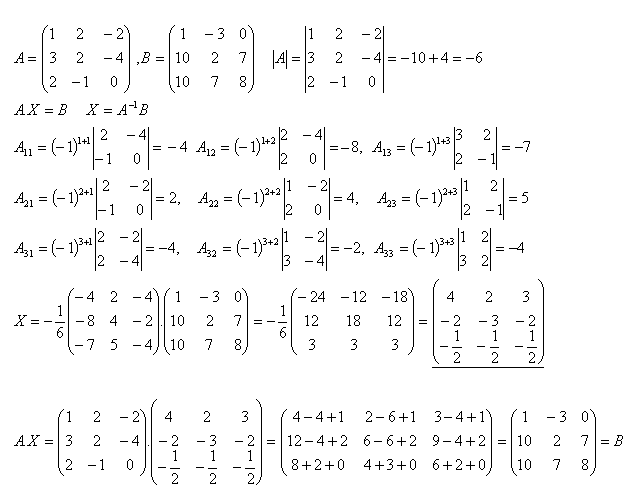
18.Erklären Sie das Verfahren zur Lösung eines linearen Gleichungssystems mittels inverser Matrix.
Lösung:
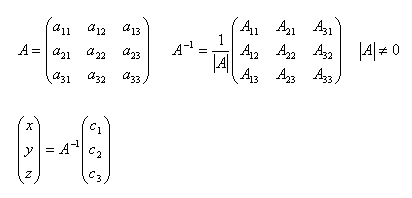
19.Lösen Sie mithilfe der inversen Matrix das Gleichungssystem:
Lösung:
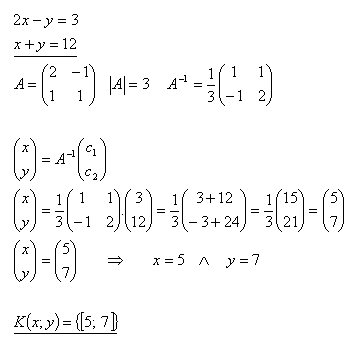
20.Lösen Sie mithilfe der inversen Matrix das Gleichungssystem:
Lösung:
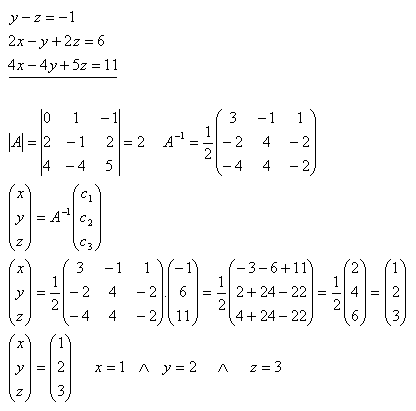
21.Lösen Sie mithilfe der inversen Matrix das Gleichungssystem:
Lösung:
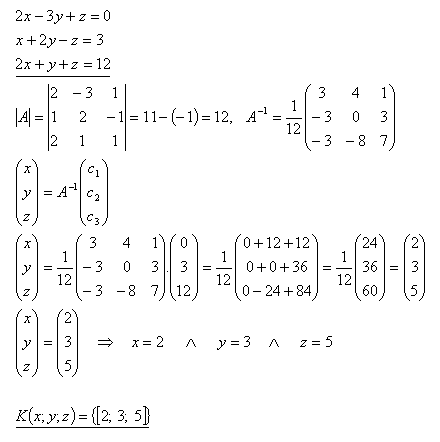
22.Lösen Sie mithilfe der inversen Matrix das Gleichungssystem:
Lösung:
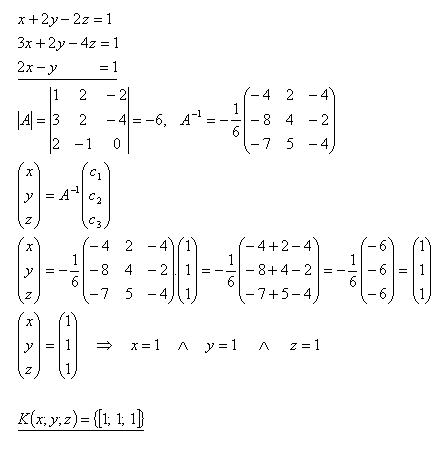
23.Erklären Sie das Konzept des „Rangs einer Matrix“ und die Bedingungen zur Lösung eines linearen Gleichungssystems mittels des Gauß-Verfahrens.
Lösung:
Der Rang einer Matrix h ist die Zahl, die die maximale Anzahl linear unabhängiger Zeilen der Matrix angibt. Der Rang einer Matrix ändert sich nicht, wenn:
- a.) wir die Reihenfolge der Zeilen vertauschen
- b.) wir eine beliebige Zeile mit einer von Null verschiedenen Zahl multiplizieren
- c.) wir zu einer Zeile eine andere Zeile addieren
- d.) wir zu einer Zeile eine lineare Kombination anderer Zeilen addieren
- e.) wir eine Zeile entfernen, die eine lineare Kombination anderer Zeilen ist
- f.) wir eine Nullzeile entfernen
- g.) wir Zeilen durch Spalten ersetzen (es entsteht die „transponierte Matrix“)
Die genannten Eigenschaften des Rangs gelten auch für Spalten.
Frobenius-Theorem:
Ein lineares Gleichungssystem hat nur dann eine Lösung, wenn der Rang der Koeffizientenmatrix h gleich dem Rang der erweiterten Matrix h/ ist.
h = h/
a.) h = h/ und h = n eindeutige Lösung
b.) h = h/ und h < n unendlich viele Lösungen (wobei n die Anzahl der Unbekannten ist)
24.Lösen Sie das Gleichungssystem nach dem Gauß-Verfahren:
Lösung:
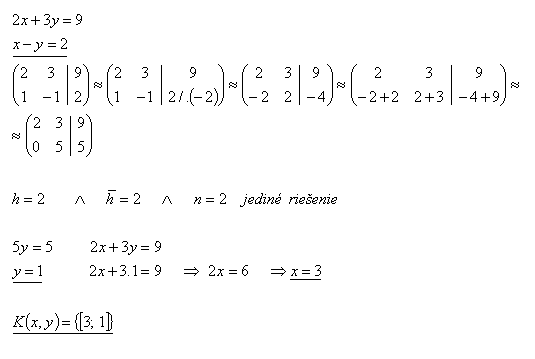
25.Lösen Sie das Gleichungssystem nach dem Gauß-Verfahren:
Lösung:
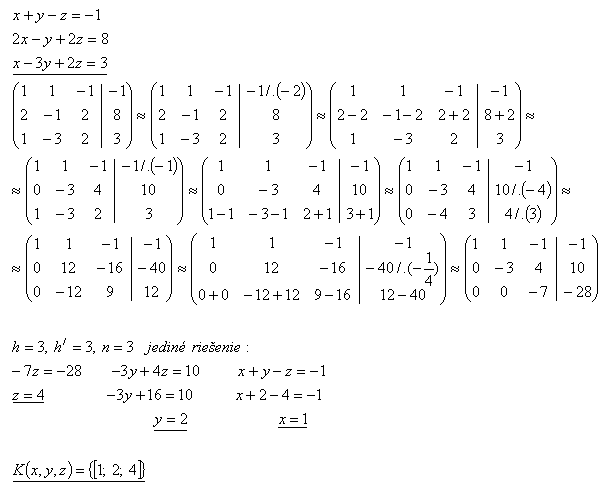
26.Lösen Sie das lineare Gleichungssystem mittels Gauß-Verfahren:
x + 2y + 3z = 0
2x – y + z = 3
3x + y – z = 5
Lösung:
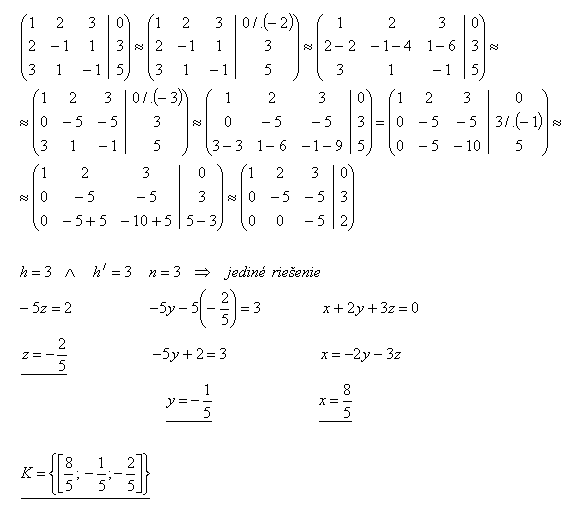
27.Lösen Sie das Gleichungssystem nach dem Gauß-Verfahren:
Lösung:
