sk|cz|en|

Mathematik

Bestimmtes Integral – Leibniz- und Newton-Verfahren

1.Was sind die Eigenschaften eines bestimmten Integrals?

Lösung:

Leibniz–Newton-Formel:

Sei f(x) eine stetige Funktion auf dem Intervall <a,b>, (wobei a die untere Grenze und b die obere Grenze des Intervalls ist). Dann gilt die Leibniz–Newton-Formel:


∫abf(x)dx=[F(x)]ab=F(b)−F(a),a<b

Eigenschaften:

1.)

∫abf(x)dx=−∫baf(x)dx

2.)

∫abf(x)dx=∫acf(x)dx+∫cbf(x)dx,a<c<b


2.Berechne die Integrale:

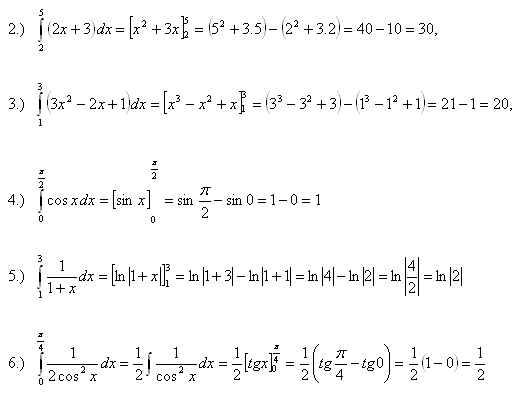
urcity-integral-leibniz–newtonova-metoda-2.gif 

Lösung:

urcity-integral-leibniz–newtonova-metoda-2.gif 

3.Berechne die Integrale:

urcity-integral-leibniz–newtonova-metoda-3z

Lösung:

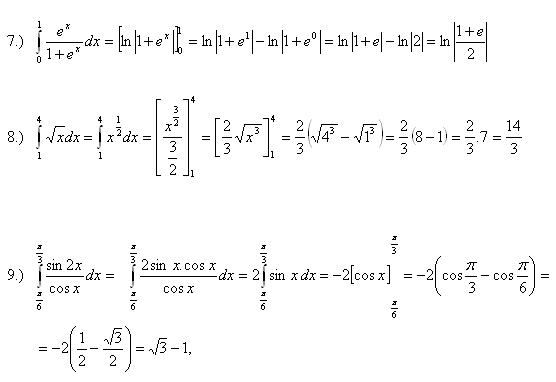
urcity-integral-leibniz–newtonova-metoda-3r  

4.Berechne die Integrale:

urcity-integral-leibniz–newtonova-metoda-4z

Lösung:

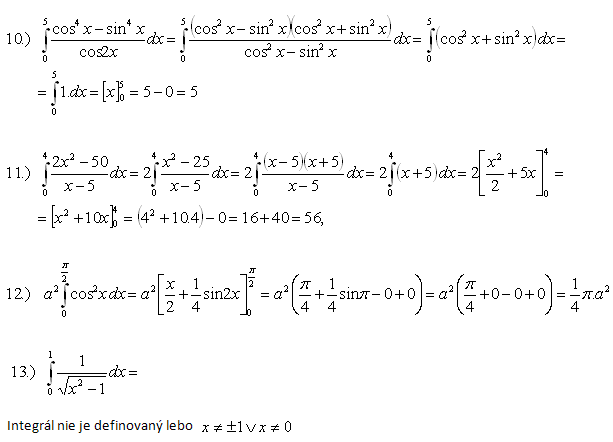
urcity-integral-leibniz–newtonova-metoda-4r

Das Integral ist nicht definiert, weilx≠±1∨x≠0