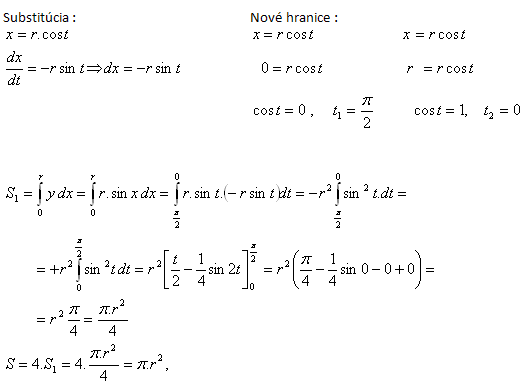Quadratur
1.Erklären Sie den Begriff „Quadratur“
Lösung:
Quadratur ist die Berechnung der Fläche einer ebenen Figur, die von der x-Achse, zwei Geraden parallel zur y-Achse an den Punkten x1 = a, x2 = b sowie einer (geraden oder gekrümmten) Linie mit der Gleichung y = f(x) begrenzt wird.
2.Leiten Sie mit Hilfe eines bestimmten Integrals die Formel zur Berechnung der Fläche her von
Lösung:
a) Quadrat
Das Quadrat wird von der x-Achse, der Geraden y = a und den zu y-Achse parallelen Geraden an den Punkten a = 0, b = a begrenzt.
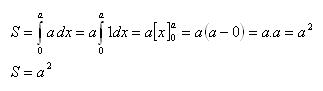
b) Rechteck
Das Rechteck wird von der x-Achse, der Geraden y = b und den zu y-Achse parallelen Geraden an den Punkten a = 0, b = a begrenzt.
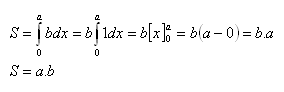
3.Leiten Sie mit Hilfe eines bestimmten Integrals die Formel zur Berechnung der Fläche her von
- a) einem gleichschenkligen Dreieck
- b) einem gleichschenkligen Trapez
Lösung:
a) Gleichschenkliges Dreieck
Das gleichschenklige Dreieck hat eine Grundseite a und eine Höhe v. Sei S1 die Hälfte der Fläche dieses Dreiecks, die von der x-Achse, den parallelen Geraden zur y-Achse an den Punkten a = 0, b = v sowie der Geraden begrenzt wird.
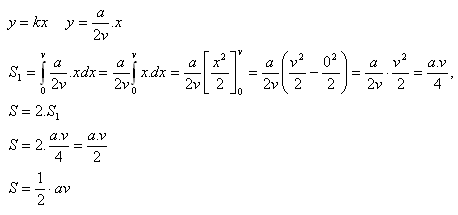
b) Gleichschenkliges Trapez
Das gleichschenklige Trapez hat eine obere Grundseite a, eine untere Grundseite b und eine Höhe v. Sei S1 die Hälfte der Fläche dieses Trapezes, die von der x-Achse, den parallelen Geraden zur y-Achse an den Punkten a = 0, b = v sowie der Geraden begrenzt wird.
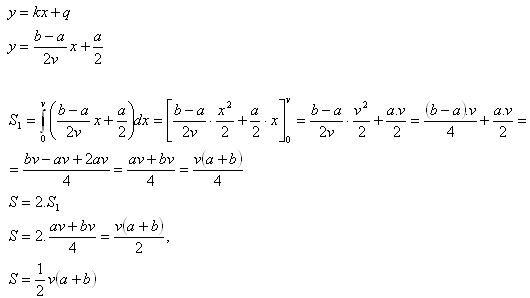
4.Berechnen Sie die Fläche der Figur, die durch die Parabel y = x2 + 1 und die Gerade y = 5 begrenzt wird.
Lösung:
Die Schnittpunkte der Geraden y1 = 5 und der Parabel y2 = x2 + 1 sind die Grenzen des Integrals.
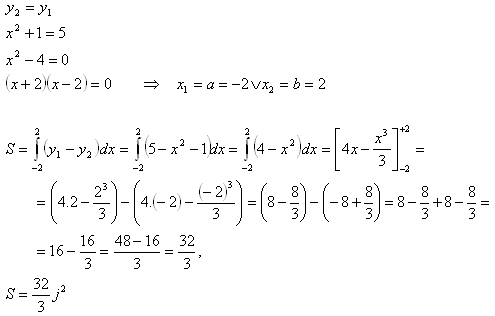
5.Berechnen Sie mit Hilfe eines bestimmten Integrals die Fläche der ebenen Figur, die durch die Parabeln
y = 6 – 4x + x2 und y = –3 + 8x – 2x2 begrenzt wird.
Lösung:
Die Schnittpunkte der Parabeln y1 = 6 – 4x + x2 und y2 = –3 + 8x – 2x2 sind die Grenzen des Integrals.
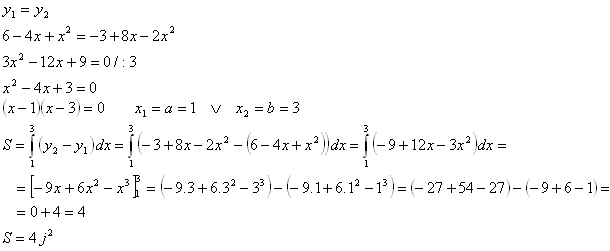
6.Leiten Sie die Formel zur Berechnung der Fläche eines Kreises mit Radius r her.
Lösung:
Zunächst zeigen wir, dass die Gleichungen x = r·cos t und y = r·sin t die Parameterdarstellung eines Kreises sind.
Beweis:
x2 + y2 = r2
r2cos2t + r2sin2t = r2
r2(cos2t + sin2t) = r2
r2·1 = r2
r2 = r2 – die Aussage stimmt
S1 ist ein Viertel des Kreises, das von der x-Achse, der y-Achse (x = 0) und dem Kreisbogen y = r·sin t begrenzt wird.
Substitution Neue Grenzen