Linsen

1. Erkläre die Bildentstehung mit Linsen.

Lösung:

Eine Linse ist ein homogener Körper, der begrenzt ist durch:

zwei kugelförmige Flächen
eine kugelförmige Fläche und eine Ebene

Eine Linse erzeugt ein Bild durch Lichtbrechung. Es gibt zwei Arten von Linsen:

sammelnd (konvex)
zerstreuend (konkav)

Dünne Linse mit gleichen Krümmungsradien:

f = Brennweite
r = 2·f = Krümmungsradius
a = Gegenstandsweite
á = Bildweite
y = Gegenstandshöhe
ý = Bildhöhe

Vergrößerung des Bildes:

Z = \frac{\hat{y}}{y} = -\frac{\hat{a}}{a} = -\frac{f}{a - f} = \frac{a}{a - f}

Gegenstandsraum = Raum vor der Linse (linke Seite)
Bildraum = Raum hinter der Linse (rechte Seite)

Vorzeichenkonvention:

r₁, r₂ positiv (negativ) – kugelförmige Flächen konvex (konkav)
a positiv – Gegenstand im Gegenstandsraum
á positiv (negativ) – Bild im Bildraum (Gegenstandsraum)
y, ý positiv (negativ) – oberhalb (unterhalb) der optischen Achse

Linsengleichung:

$\frac{1}{a} + \frac{1}{\hat{a}} = \frac{1}{f}$

$\frac{1}{a} + \frac{1}{\hat{a}} = \frac{1}{f}$ $\frac{1}{f} = \left(\frac{n_2}{n_1} - 1\right)\left(\frac{1}{r_1} - \frac{1}{r_2}\right)$

n₂ = Brechungsindex der Linse, n₁ = Brechungsindex des umgebenden Mediums

Brechkraft einer Linse Φ:

\Phi = \frac{1}{f}, \quad [\Phi] = m^{-1} = D = diopter

Φ > 0 → Sammellinse
Φ < 0 → Zerstreuungslinse

2. Bestimme die Brennweite der Linsen, wenn ihre Brechkraft ist:

a) φ = 2D
b) φ = -12D

Lösung:

Analyse:

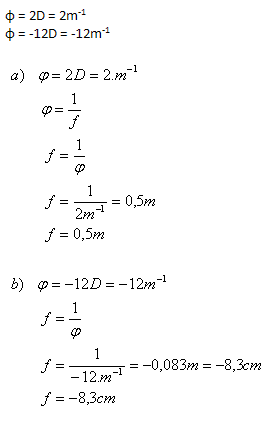
Die Brennweite der Linsen beträgt 0.5m und –8.3cm.

3. Bestimme die Brechkraft einer bikonvexen Linse mit r₁ = r₂ = 0.4m aus Steinsalz (n₂ = 1.537) in Luft (n₁ = 1) und in Schwefelkohlenstoff (n₁ = 1.609).

Lösung:

Analyse:

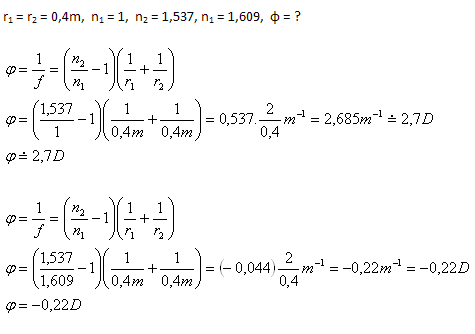
Die Brechkraft der Linse in Luft beträgt 2.7D, in Schwefelkohlenstoff –0.22D.

4. In welchem Abstand vom Objektiv (Sammellinse) muss der Projektionsschirm aufgestellt werden, damit das Bild 50-fach vergrößert wird? Die Brennweite der Linse ist f = 10cm. Für ein reelles Bild, das von einer Sammellinse erzeugt wird, gilt Z < 0.

Lösung:

Analyse:

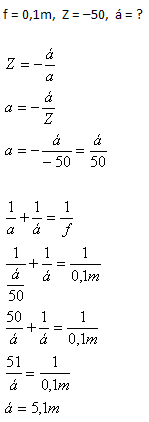
Der Projektionsschirm sollte 5.1m vom Objektiv entfernt aufgestellt werden.

5. Der Abstand zwischen einer Kerze und einer Wand beträgt 100cm. In welchem Abstand von der Kerze (zwischen Kerze und Wand) soll eine Sammellinse mit f = 9cm aufgestellt werden, damit auf der Wand ein scharfes Bild entsteht?

Lösung:

Analyse:

a = Abstand von der Kerze zur Linse
á = Abstand von der Linse zur Wand
a + á = 100cm, f = 9cm

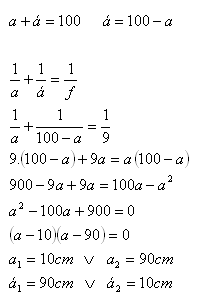
Die Linse sollte 10cm von der Kerze und 90cm von der Wand entfernt stehen (oder umgekehrt).

6. Vor einer Sammellinse steht eine Kerze mit einer Flammenhöhe von 5cm. Die Linse erzeugt auf dem Schirm ein Bild mit einer Flammenhöhe von 15cm. Wird die Kerze um 1.5cm von der Linse weg bewegt, entsteht erneut ein scharfes Bild auf dem Schirm mit einer Höhe von 10cm. Bestimme die Brennweite der Linse.

Lösung:

Analyse:

$y_{1} = 5 cm, y_{1'} = 15 cm, y_{2} = 5 cm, y_{2'} = 10 cm, f = ?$

Vor dem Verschieben:

$|Z_1| = \frac{y'_1}{y_1} = \frac{15\text{ cm}}{5\text{ cm}} = 3, \qquad a'_1 = 3a, \qquad a = \text{object distance}$

$\frac{1}{a_1} + \frac{1}{a'_1} = \frac{1}{f}$

$\frac{1}{a} + \frac{1}{3a} = \frac{1}{f}$

Nach dem Verschieben:

$|Z_2| = \frac{y'_2}{y_2} = \frac{10\text{ cm}}{5\text{ cm}} = 2, \qquad a_2 = a + 1.5, \qquad a'_2 = 2a_2 = 2(a + 1.5)$

$\frac{1}{a_2} + \frac{1}{a'_2} = \frac{1}{f}$

$\frac{1}{a + 1.5} + \frac{1}{2(a + 1.5)} = \frac{1}{f}$

$\frac{1}{f} = \frac{1}{f}$

$\frac{1}{a} + \frac{1}{3 a} = \frac{1}{a + 1.5} + \frac{1}{2 (a + 1.5)}$

$\frac{1}{a} + \frac{1}{3a} = \frac{1}{a + 1.5} + \frac{1}{2(a + 1.5)}$ $\frac{4}{3a} = \frac{3}{2(a + 1.5)}$

$8(a + 1.5) = 9a$

$a = 12\text{ cm}, \qquad \frac{1}{f} = \frac{4}{3a}$

$f = \frac{3a}{4} = \frac{3 \cdot 12\text{ cm}}{4} = 9\text{ cm}$

$f = 9\text{ cm$

Die Brennweite der Linse ist f = 9cm.

7. Eine dünne Glaslinse hat in Luft (n = 1) einen Brechungsindex n₁ = 1.7 und eine Brechkraft φ = 4D. Welche Brechkraft hat dieselbe Linse, wenn sie in eine Flüssigkeit mit Brechungsindex n₂ = 1.85 getaucht wird?

Lösung:

Analyse:

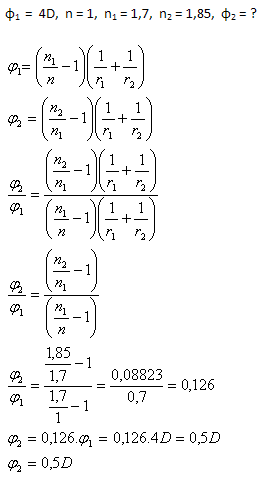
Die Brechkraft der Linse in der Flüssigkeit ist φ = 0.5D. Es ist eine Sammellinse.

8. Ein zylindrischer Strahlenbündel, der zur optischen Achse parallel ist, trifft auf eine Zerstreuungslinse. Der Bündeldurchmesser beträgt 5cm. Auf einem 20cm hinter der Zerstreuungslinse aufgestellten Schirm entsteht ein kreisförmiger Fleck mit einem Durchmesser von 15cm. Bestimme die Brennweite der Zerstreuungslinse.

Lösung:

Analyse:

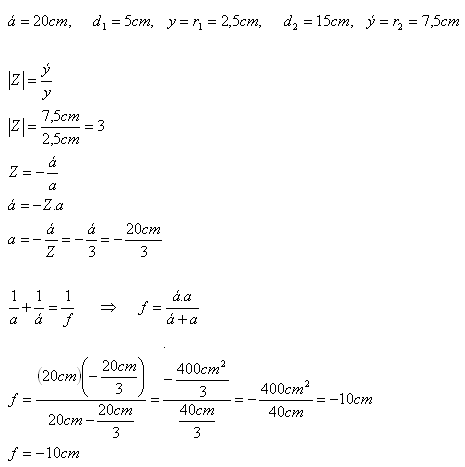
Die Brennweite der Zerstreuungslinse ist f = –10cm.

9. Eine dünne Zerstreuungslinse hat eine Brennweite von 20cm. Eine Kerze wird vor der Linse zuerst in 20cm, dann in 30cm Abstand aufgestellt. Berechne den Abstand zwischen den von der Linse erzeugten Bildern der Kerzenflamme (f < 0).

Lösung:

Analyse:

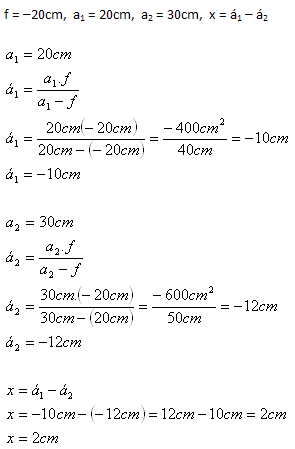
Der Abstand zwischen den von der Zerstreuungslinse erzeugten Bildern beträgt x = 2cm.

10. Eine Meniskuslinse mit einem Brechungsindex von 1.6 hat eine Brechkraft von φ = 1.25m^-1. Eine der Linsenflächen hat einen Krümmungsradius von 120mm. Bestimme den Krümmungsradius der anderen Fläche.

Lösung:

Analyse:

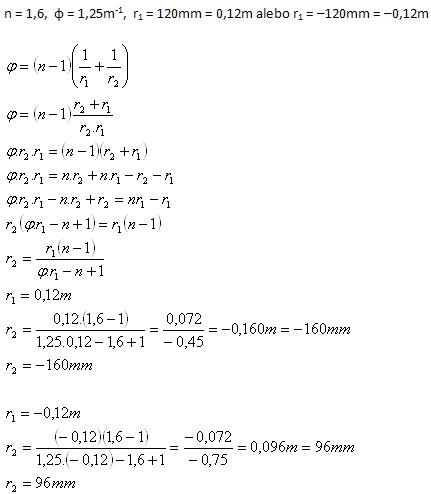
Ist r₁ = 120mm, dann ist r₂ = –160mm.
Ist r₁ = –120mm, dann ist r₂ = 96mm.

11.Isaac Newton veröffentlichte in seinem Werk *Optics* (1704) die Linsengleichung in der Form f² = ( a – f ).( a^/ - f ). Zeigen Sie, dass sie mit der heute verwendeten Gleichung identisch ist.

Lösung:

sosovky-11

12.Wir betrachten durch eine Zerstreuungslinse mit einer Brennweite von 10 cm einen Gegenstand, der 30 cm von der Linse entfernt ist. Wo und welche Art von Bild werden wir sehen?

Lösung:

Analyse:

sosovky-12

Das Bild ist verkleinert, aufrecht, virtuell und befindet sich 7,5 cm vor der Zerstreuungslinse.

13.In welcher Entfernung von einer Zerstreuungslinse mit φ = -5D muss ein Gegenstand platziert werden, um ein vierfach verkleinertes Bild zu erhalten?

Lösung:

sosovky-13

Der Gegenstand muss in einer Entfernung von 0,6 m von der Linse platziert werden.

14.Der Gegenstand befindet sich in einer Entfernung von 10 cm vor einer Sammellinse mit f_S = 20 cm. Wie ändert sich die Bildgröße, wenn wir die Sammellinse durch eine Zerstreuungslinse mit f_R = –20 cm ersetzen?

a_S = 10 cm, a_R = 10 cm, f_S = 20 cm., f_R = –20 cm

Lösung:

a_S = 10 cm, a_R = 10 cm, f_S = 20 cm., f_R = –20 cm

Sammellinse: Zerstreuungslinse:

sosovky-14

Wenn wir die Sammellinse durch eine Zerstreuungslinse ersetzen, wird die Bildgröße um das 3-fache kleiner.

15.Die Entfernung des Gegenstandes von einer Zerstreuungslinse ist fünfmal größer als ihre Brennweite. Bestimmen Sie die Eigenschaften des Bildes.

Lösung:

sosovky-15

Das Bild ist aufrecht, virtuell und 6-fach verkleinert.

16.Eine Meniskuslinse aus Glas (n₂ = 1,5) hat eine Brennweite von 24 cm. Wie groß sind die Krümmungsradien beider optischer Flächen, wenn die konkave Fläche den doppelt so großen Krümmungsradius wie die konvexe hat?

Lösung:

sosovky-16

Die Linse hat die Krümmungsradien r₁ = 6 cm, r₂ = –12 cm.

17.Eine konvexe Glaslinse hat in Luft eine Brennweite von f₁ = 20 cm. Wie groß ist ihre Brennweite f₂ im Wasser?

Lösung:

sosovky-17

Die Brennweite der Linse im Wasser beträgt f₂ = 80 cm.

18.Eine plankonvexe Linse, deren sphärische Fläche einen Radius von 15 cm hat, erzeugt ein reelles, 9-fach vergrößertes Bild. Wie groß sind die Abstände des Gegenstands und des Bildes von der Linse, wenn n_S = 1,5?

Lösung:

sosovky-18

Der Abstand des Gegenstands von der Linse beträgt 33,3 cm, der des Bildes 300 cm.

19.Bestimmen Sie die Brennweite eines Systems aus zwei sich berührenden dünnen Linsen mit Brennweiten von 10 cm und 40 cm, wenn:

a.) beide Linsen Sammellinsen sind
b.) die erste Linse Sammellinse, die zweite Zerstreuungslinse ist.

Lösung:

Beide Linsen Sammellinsen: Erste Linse Sammellinse, zweite Zerstreuungslinse:

sosovky-19

Die Brennweite des Systems beträgt im ersten Fall 8 cm, im zweiten 13,3 cm.

20.Erklären Sie die Bessel-Methode zur Bestimmung der Brennweite einer Sammellinse. F.W. Bessel (1787–1846) war ein deutscher Physiker.

Lösung:

sosovky-20gif

Die Werte l und d müssen in einem entsprechend vorbereiteten Experiment gemessen werden.

Physik

Linsen

Adblock detected