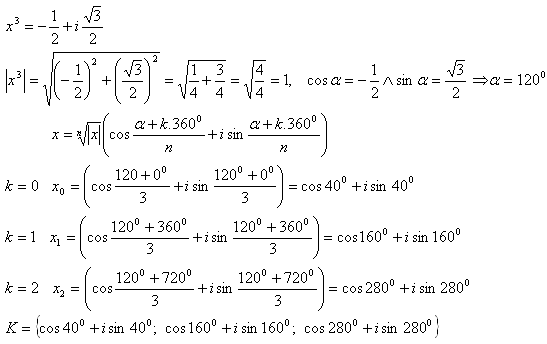Lösen von Gleichungen in der Menge der komplexen Zahlen
1.Löse in der Menge C die Gleichung:
Lösung:
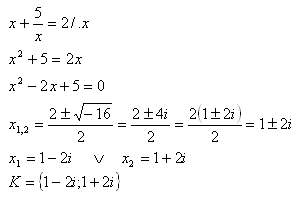
2.Löse in der Menge C die Gleichung:
Lösung:
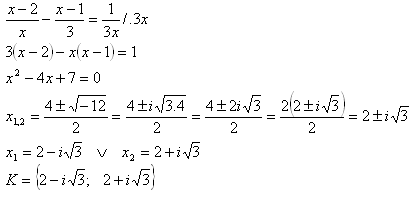
3. Löse in der Menge C die Gleichung:
Lösung:
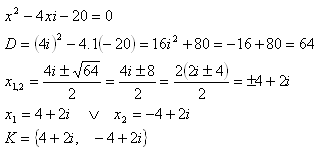
4.Welche quadratische Gleichung hat die Nullstelle x1 = 1 – i
Lösung:
Wenn x1 = 1 – i ist, dann ist x2 = 1 + i.
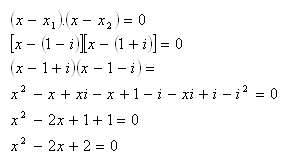
5.Welche quadratische Gleichung hat die Nullstellen
Lösung:
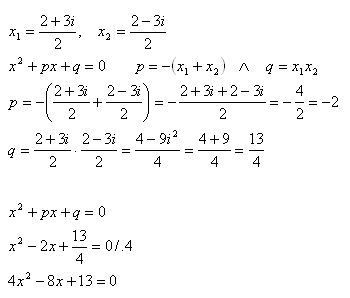
Die Gleichung mit den gegebenen Nullstellen ist 4x2 - 8x + 13 = 0
6.Löse in der Menge C die Gleichung:
x4 – 1 = 0
Lösung:
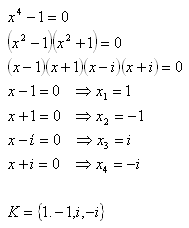
7.Löse in der Menge C die Gleichung:
x6 – 64 = 0
Lösung:
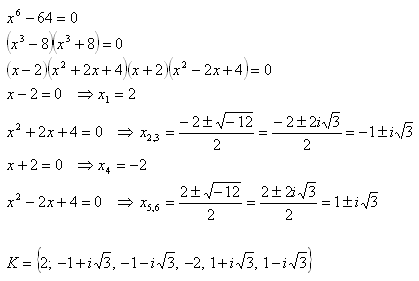
8.Löse in der Menge C die Gleichung:
5x3 – 11x2 + 11x – 5 = 0
Lösung:
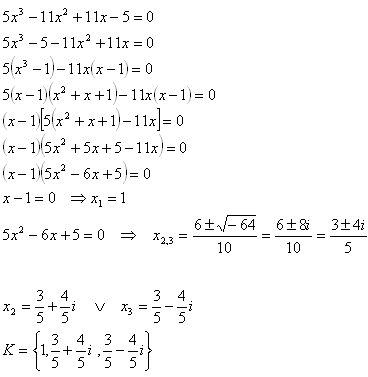
9. Löse in der Menge C die Gleichung x4 – 10x2 = 96. Wähle eine geeignete Substitution.
Lösung:
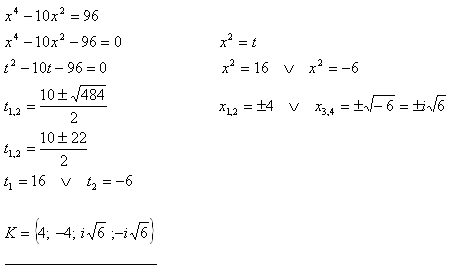
10.Löse in der Menge C die Gleichung 5(x – 3)4 + 8(x – 3)2 = 112. Wähle eine geeignete Substitution.
Lösung:
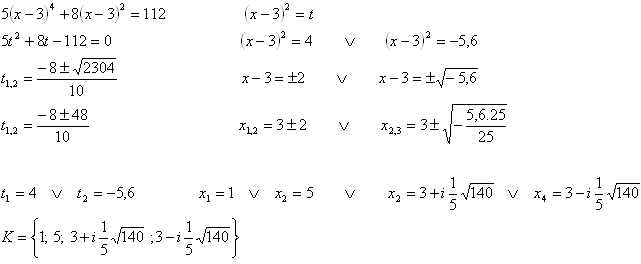
11.Löse in der Menge C die Gleichung:
Lösung:
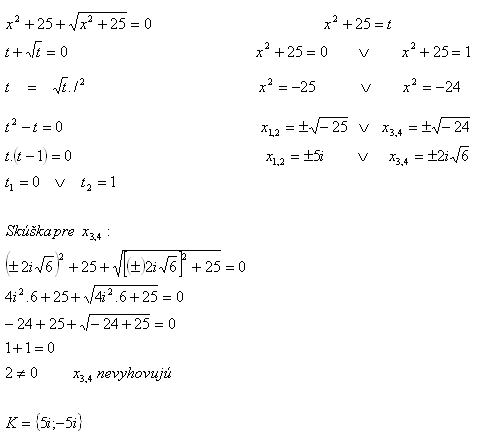
12. Löse in der Menge C die Gleichung x3 – x2 + x = 0. Zeige, dass: x1 + x2 + x3 = 1 und x1·x2·x3 = 0
Lösung:
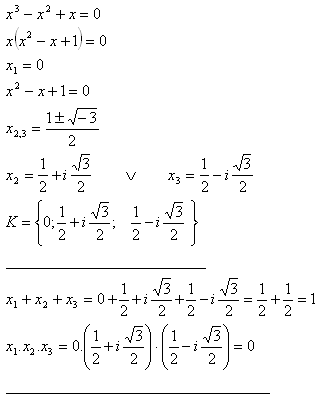
13.Löse in der Menge C die Gleichung 16x4 – 81 = 0. Verwende die trigonometrische (Polardarstellung) einer komplexen Zahl.
Lösung:
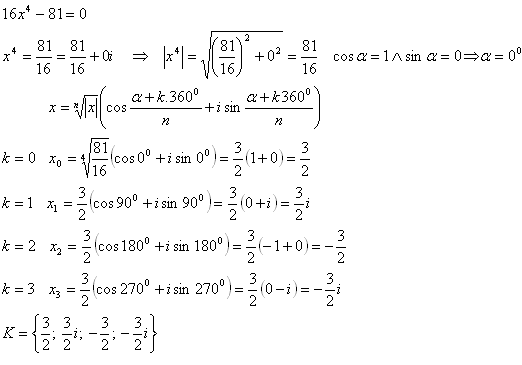
14.Löse in der Menge C die Gleichung x6 + 64 = 0. Verwende die trigonometrische (Polardarstellung) einer komplexen Zahl.
Lösung:
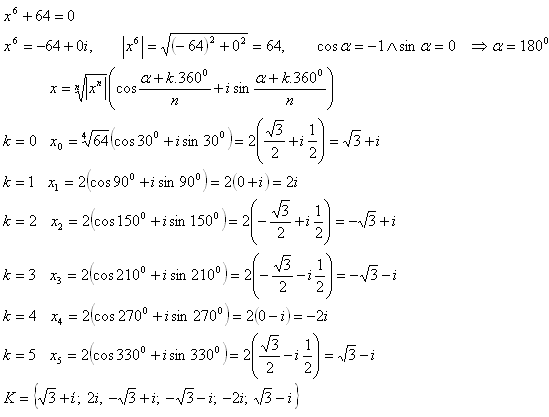
15.Löse in der Menge C die Gleichung:
Lösung: