sk|cz|en|

Physik

Lichtinterferenz

1.Erklären Sie das Wesen und die Methoden der Lichtinterferenz.

Lösung:

Interferenz entsteht durch die Überlagerung zweier Lichtwellen, die kohärent sein müssen. Sie müssen die gleiche Frequenz und einen konstanten Phasenunterschied haben. Die Kohärenzbedingung kann von Lichtwellen aus zwei verschiedenen
Quellen nicht erfüllt werden. Sie kann erreicht werden, indem die Lichtwelle einer Quelle in zwei kohärente Wellen aufgeteilt wird. Dies kann erreicht werden:

  • a) durch Reflexion der Welle an einem Hindernis – Interferenz durch Reflexion
  • b) durch Beugung der Welle an einem Hindernis oder einem Spalt – Interferenz durch Beugung


Interferenzmaximum – Stelle, an der das Licht durch Interferenz verstärkt wird
Interferenzminimum – Stelle, an der das Licht durch Interferenz geschwächt oder ausgelöscht wird.
                              

Interferenz Maximum Minimum
Durch Reflexion             2nd=(2k−1)λ22 n d = (2k - 1)\frac{\lambda}{2}             2nd=2kλ22 n d = 2k \frac{\lambda}{2}
Durch Beugung             dsin⁡α=2kλ2d \sin \alpha = 2k \frac{\lambda}{2}             dsin⁡α=(2k−1)λ2d \sin \alpha = (2k - 1)\frac{\lambda}{2}

k = 1,2,3,....

2.Bestimmen Sie die Dicke der Wand einer Seifenblase (n = 1.33), wenn weißes Licht darauf fällt. Das Interferenzmaximum erster Ordnung wird im grünen Licht beobachtet (fG = 5.7·1014Hz).

Lösung:

Analyse:

n = 1.33, fG = 5.7·1014Hz,  c = 3·108m·s-1,  d = ?  k = 1

Dabei wird die Beziehung für das Interferenzmaximum erster Ordnung bei Reflexion verwendet.

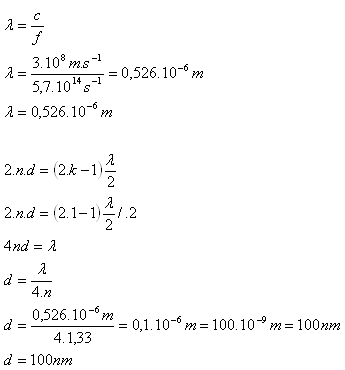
physics-interference-light-2.gif 

Die Dicke der Seifenblasenwand beträgt d = 100 nm.

3.Die Dicke eines Ölfilms beträgt d = 2.4·10-7m und der Brechungsindex des Öls ist n = 1.5. Welche Farben des reflektierten Lichts werden durch Interferenz ausgelöscht?

Lösung:

Analyse:

Dies ist ein Interferenzminimum bei Reflexion.

d = 2.4·10⁻⁷ m, n = 1.5, λ = ?

2nd=kλ2 n d = k \lambda
λ=2ndk\lambda = \dfrac{2 n d}{k}

k = 1 ⇒ λ=2⋅1.5⋅2.4⋅10−7 m1=7.2⋅10−7 m\lambda = \dfrac{2 · 1.5 · 2.4·10^{-7}\,\text{m}}{1} = 7.2·10^{-7}\,\text{m} – rotes Licht

k = 2 ⇒ λ=2⋅1.5⋅2.4⋅10−7 m2=3.6⋅10−7 m\lambda = \dfrac{2 · 1.5 · 2.4·10^{-7}\,\text{m}}{2} = 3.6·10^{-7}\,\text{m} – violettes Licht

k = 3 ⇒ λ=2⋅1.5⋅2.4⋅10−7 m3=2.4⋅10−7 m – Ultraviolettstrahlung

Durch Interferenz bei Reflexion werden rotes und violettes Licht sowie unsichtbare Ultraviolettstrahlung ausgelöscht.

4.Eine Glasplatte mit dem Brechungsindex n = 1.5 und der Dicke d = 0.25μm wird mit Licht beleuchtet. Welche Wellenlänge wird im reflektierten Licht maximal verstärkt?

Lösung:

Analyse:

Interferenzmaximum bei Reflexion:

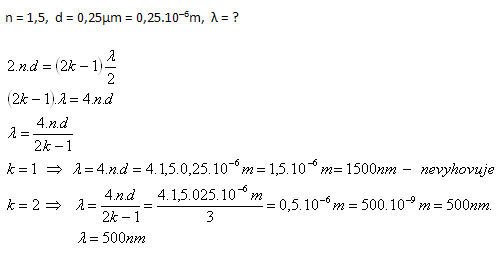
physics-interference-light-4.gif 

Die Wellenlänge des Lichts muss λ = 500nm sein.

5.Wie viele Interferenzmaxima entstehen bei der Beugung von Licht an einem Gitter mit 5000 Linien pro 1 cm, wenn oranges Licht mit λ = 600nm darauf fällt?

Lösung:

Analyse:

5000 Linien pro 1 cm, λ = 600 nm = 600·10⁻⁹ m, α = ?

Gitterkonstante d:

d=10−2 m5⋅103=0.2⋅10−5 md = \frac{10^{-2}\,\text{m}}{5\cdot10^{3}} = 0.2\cdot10^{-5}\,\text{m}

dsin⁡α=kλd \sin\alpha = k \lambda

sin⁡α=kλd\sin\alpha = \frac{k \lambda}{d}

k=1⇒sin⁡α1=1⋅600⋅10−9 m0.2⋅10−5 m=3000⋅10−4=0.3⇒α1=17.45∘k = 1 \Rightarrow \sin\alpha_1 = \dfrac{1\cdot600\cdot10^{-9}\,\text{m}}{0.2\cdot10^{-5}\,\text{m}} = 3000\cdot10^{-4} = 0.3 \Rightarrow \alpha_1 = 17.45^\circ

k=2⇒sin⁡α2=2⋅600⋅10−9 m0.2⋅10−5 m=6000⋅10−4=0.6⇒α2=36.87∘

k=3⇒sin⁡α3=3⋅600⋅10−9 m0.2⋅10−5 m=9000⋅10−4=0.9⇒α3=64.15∘k = 3 \Rightarrow \sin\alpha_3 = \dfrac{3\cdot600\cdot10^{-9}\,\text{m}}{0.2\cdot10^{-5}\,\text{m}} = 9000\cdot10^{-4} = 0.9 \Rightarrow \alpha_3 = 64.15^\circ

k=4⇒sin⁡α4=4⋅600⋅10−9 m0.2⋅10−5 m=12000⋅10−4=1.2k = 4 \Rightarrow \sin\alpha_4 = \dfrac{4\cdot600\cdot10^{-9}\,\text{m}}{0.2\cdot10^{-5}\,\text{m}} = 12000\cdot10^{-4} = 1.2 – undefiniert. 

Es entstehen drei Interferenzmaxima. Das Maximum 4. Ordnung existiert nicht.

6.Ein Beugungsgitter mit 100 Linien pro 1 mm wird senkrecht mit rotem Licht (λ = 700nm) beleuchtet. Bestimmen Sie den Abstand „h“ zwischen dem ersten und dritten hellen Streifen auf einem Schirm, der in der Entfernung l = 1.5m von der Lichtquelle steht.

Lösung:

Analyse:

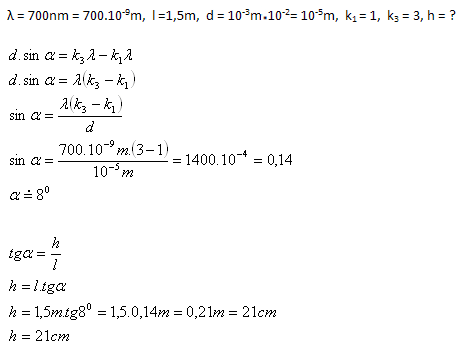
 physics-interference-light-6.gif

Der erste und der dritte helle Streifen auf dem Schirm werden einen Abstand von h = 21 cm voneinander haben.

7.Wie viele Linien pro 1 mm besitzt ein optisches Gitter, wenn Licht mit der Wellenlänge λ = 589nm im zweiten Maximum um den Winkel α = 43015‘ von der Richtung senkrecht zur Gitterebene abgelenkt wird?

Lösung:

Analyse:

physics-interference-light-7.gif 

Das optische Gitter hat 582 Linien pro Millimeter.