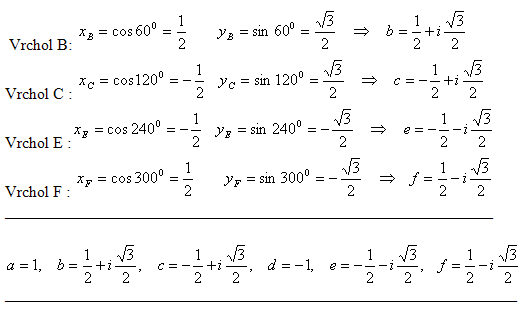Eigenschaften komplexer Zahlen
1.Gegeben seien die komplexen Zahlen a = 1+2i , b = 2 – i. Bestimme a + b, a – b, a·b, a / b, |a|, ferner
Bestimme, ob die Zahl
eine komplexe Einheit ist.
Lösung:
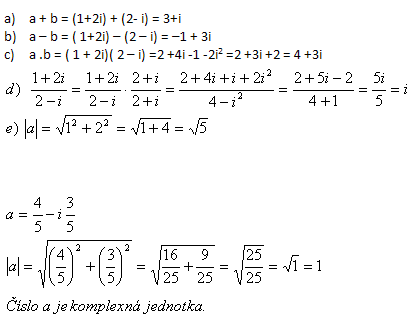
Die Zahl a ist eine komplexe Einheit
2.Schreibe die Zahl
- a) in trigonometrischer Form
- b) in Exponentialform
- c) berechne a5
- d) berechne √a
Lösung:
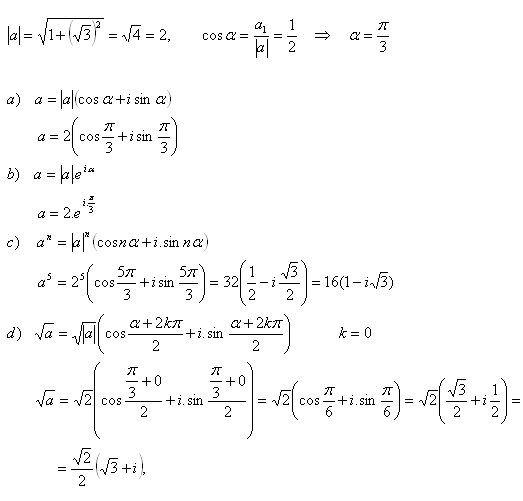
3.Berechne:
Lösung:
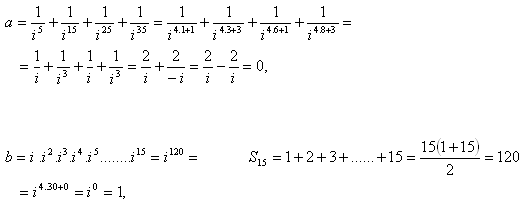
4.Berechne:
Lösung:
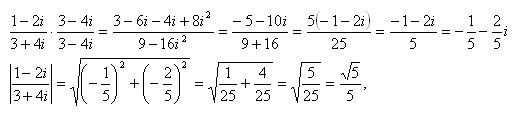
5.Bestimme reelle Zahlen x , y so, dass:
(3 – 2i)·x + (5 – 7i)·y = 1 + 3i
Lösung:
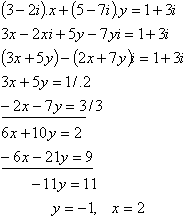
6.Berechne:
Lösung:
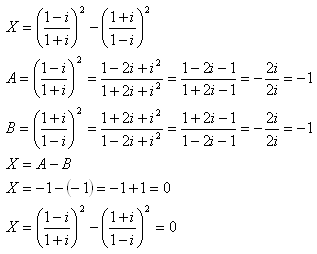
7. Ein Quadrat hat sein Zentrum im Ursprung der gaußschen Zahlenebene, ein Eckpunkt ist das Bild der komplexen Zahl a = 4 + 3i.
- a) Welche komplexen Zahlen stellen die übrigen Eckpunkte dar?
- b) Bestimme den Flächeninhalt dieses Quadrats
Lösung:
a) Die gesuchten komplexen Zahlen müssen folgende Bedingungen erfüllen:
-
Ihr Betrag ist gleich ∣a∣
-
Jede liegt in einem anderen Quadranten der gaußschen Zahlenebene
Die komplexen Zahlen, die die geforderten Bedingungen erfüllen, sind:
b) Flächeninhalt des Quadrats
8.Berechne die Länge der Seitenhalbierenden tc des Dreiecks ΔABC, wenn seine Eckpunkte A,B,C die Bilder der komplexen Zahlen a = –1 –i , b = –5 + 7i , c = 9 + 8i sind.
Lösung:
Die Länge der Seitenhalbierenden tc ist die Länge der Strecke CS, wobei S der Mittelpunkt der Strecke AB ist
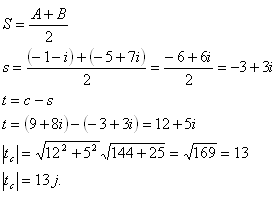
Die Seitenhalbierende tc hat die Länge 13 LE.
9.Ein regelmäßiges Sechseck ABCDEF hat das Zentrum S im Ursprung der gaußschen Zahlenebene und den Eckpunkt A im Bild der komplexen Einheit auf der reellen Achse. Bestimme die komplexen Zahlen, deren Bilder an den anderen Eckpunkten des Sechsecks liegen.
Lösung:
Eckpunkt A : a = 1
Eckpunkt D : d = –1
Die übrigen Eckpunkte liegen in einzelnen Quadranten der gaußschen Zahlenebene.
Das Dreieck Δ SAB ist gleichseitig, SA = SB = AB = 1