sk|cz|en|

Physik

Reflexion und Brechung

1.Was geschieht, wenn Licht die Grenzfläche zweier Medien durchläuft?

Lösung:

Wenn Licht die Grenzfläche zweier Medien vom ersten Medium (in dem es sich mit der Geschwindigkeit v1 bewegt) in das zweite Medium (in dem es sich mit der Geschwindigkeit v2 bewegt) durchläuft, können zwei Fälle auftreten:

  • Reflexion des Lichts
  • Brechung des Lichts

Lichtreflexion:

Reflexion des Lichts tritt auf, wenn Licht auf ein Medium trifft, in das es nicht eindringen kann.

Reflexionsgesetz:
α=α′\alpha = \al 
Der Reflexionswinkel α′\alpist gleich dem Einfallswinkel α. Der reflektierte Strahl liegt in der Einfallsebene.

Totale Reflexion – Brechung des Lichts von einem optisch dichteren Medium in ein optisch weniger dichtes Medium. (β=90∘\beta = 90^\circ)

sin⁡αm=1n1,n2=1,αm=Grenzwinkel\sin \alpha_m = \frac{1}{n_1}, \quad n_2 = 1, \quad \alpha_m = \text{critical angle}

Lichtbrechung:

Brechung des Lichts tritt auf, wenn Licht in ein anderes Medium eintritt.

Brechungsgesetz (Snelliussches Gesetz):

sin⁡αsin⁡β=v1v2=n2n1\frac{\sin \alpha}{\sin \beta} = \frac{v_1}{v_2} = \frac{n_2}{n_1}

  • α\alpha = Einfallswinkel,

  • β\beta = Brechungswinkel,

  • n1n_1 = Brechungsindex des ersten Mediums,

  • n2n_2 = Brechungsindex des zweiten Mediums.

Wenn β<α\beta < \alpha, wird der Strahl zum Lot hin gebrochen.
Wenn β>α, wird der Strahl vom Lot weg gebrochen.

Absoluter Brechungsindex:

n=cv=cλf=λ0λn = \frac{c}{v} = \frac{c}{\lambda f} = \frac{\lambda_0}{\lambda}

Medium      Luft      Wasser      Eis      Glas
nn      1.00      1.33      1.31      1.51

2.Die Geschwindigkeit roten Lichts in Glas ist v1 = 199,200 km.s-1 und violetten Lichts v2 = 196,700 km.s-1. Bestimme den Brechungsindex für rotes und violettes Licht. (c = 3.108 m.s-1)

Lösung:

Analyse:

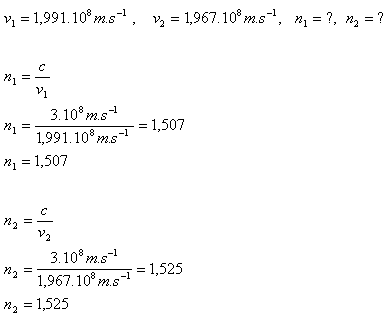
physics-reflection-and-refraction-2.gif 

Der Brechungsindex für rotes Licht in Glas ist n1 = 1.507, für violettes Licht ist er n2 = 1.525.

3.Licht trifft aus der Luft (n1 = 1) unter dem Winkel α = 680 auf die Wand eines Diamanten. Der gebrochene Strahl steht senkrecht auf dem reflektierten Strahl. Berechne:

  • den Brechungsindex des Diamanten für das verwendete Licht
  • die Lichtgeschwindigkeit im Diamanten (c = 3.108 m.s-1)

Lösung:

Analyse:

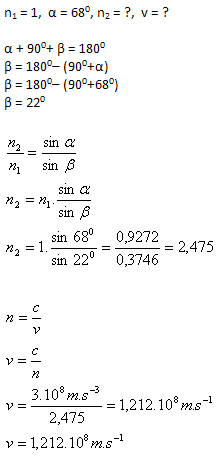
physics-reflection-and-refraction-3.gif 

  • Der Brechungsindex des Diamanten ist n2 = 2.475.
  • Die Lichtgeschwindigkeit im Diamanten ist v = 1.212·108 m.s-1.

4.Aus der Luft auf die Wasseroberfläche (n = 1.33) fallendes Licht wird unter dem Winkel β = 300 gebrochen. Bestimme den Einfallswinkel α und den Reflexionswinkel α‘.

Lösung:

Analyse:

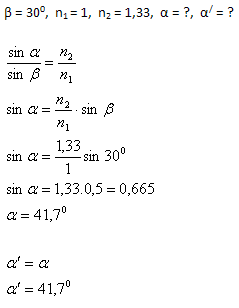
physics-reflection-and-refraction-4.gif 

Der Einfallswinkel ist α = 41.70, der Reflexionswinkel ist α‘ = 41.70.

5.Auf dem Grund eines Sees steckt ein 1 Meter langer senkrechter Pfahl, der vollständig unter der Wasseroberfläche liegt. Bestimme die Länge seines Schattens auf dem Seegrund, wenn n1(Luft) = 1, n2(Wasser) = 1.33 und die Sonne sich in der Höhe φ = 300 über der Oberfläche befindet.

Lösung:

Analyse:

l = 1m, n1(Luft) = 1, n2(Wasser) = 1.33, φ = 300, t = ? α = 900– φ = 900 – 300 = 600

Der Pfahl „l“ und der Schatten „t“ bilden ein rechtwinkliges Dreieck. Der Winkel β ist der Gegenwinkel zur Seite „t“ in diesem Dreieck.


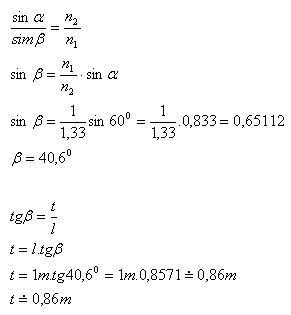
 physics-reflection-and-refraction-5.gif

Die Länge des Schattens des Pfahls beträgt 0.86m.

6.

Ein Lichtstrahl trifft aus der Luft auf eine ebene Grenzfläche von Luft und Glas, wird unter einem Winkel von 600 reflektiert und gleichzeitig unter einem Winkel von 300 in das Glas gebrochen. Bestimme die Lichtgeschwindigkeit in Glas.

Lösung:

Analyse:

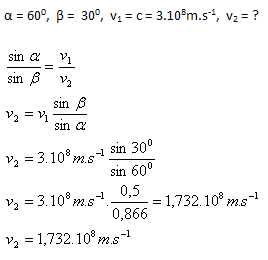
 physics-reflection-and-refraction-6.gif

Die Lichtgeschwindigkeit in Glas beträgt 1.732·108 m.s–1.

7.

Die Wellenlänge gelben Lichts in Luft beträgt λ0 = 590 nm. Wie groß ist die Wellenlänge des Lichts in Glas, wenn n = 1.5 ist? Berechne außerdem die Lichtgeschwindigkeit in diesem Medium.

Lösung:

Analyse:

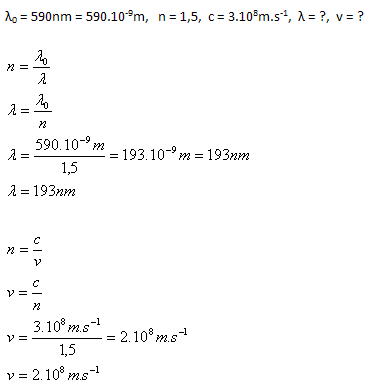
 physics-reflection-and-refraction-7.gif

Die Wellenlänge gelben Lichts in Glas ist λ = 163 nm, die Geschwindigkeit ist v = 2·108 m.s-1.

8.Unter welchem Grenzwinkel muss Licht einfallen, damit totale Reflexion auftritt, wenn Licht übergeht:

  • a) von Glas zu Luft (n1 = 1.5)
  • b) von Wasser zu Luft (n‘1 = 1.33)
  • c) von Glas zu Wasser n2(Luft) = 1

Lösung:

Analyse:

physics-reflection-and-refraction-8.gif

Die Grenzwinkel sind ungefähr 41050‘, 48049‘ und 62027‘.

9. Bestimme die Dicke der Seifenblasenwand (n = 1.33), wenn weißes Licht auf sie fällt. Das Interferenzmaximum erster Ordnung wird im grünen Licht beobachtet (fZ = 5.7·1014 Hz).

Lösung:

Analyse:

n = 1.33, fZ = 5.7·1014 Hz, c = 3·102 m.s-1, d = ? k = 1

Dies ist eine Anwendung der Beziehung für das Interferenzmaximum erster Ordnung bei Reflexion.

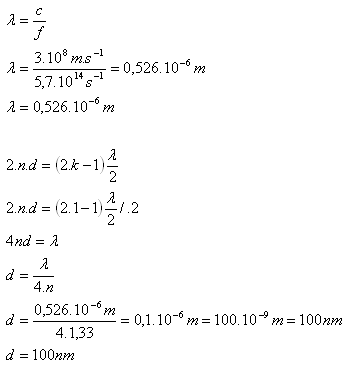
physics-reflection-and-refraction-9.gif 

Die Dicke der Seifenblasenwand ist d = 100 nm.

10.Auf dem Boden eines 32 cm tiefen Bachs liegt ein Steinchen. Ein Junge möchte es mit einem Stab berühren, den er über der Oberfläche unter einem Winkel von 450 hält. In welchem Abstand vom Steinchen wird der Stab nach dem Eintauchen den Bachboden berühren? (n1=1, n2=1.33)

Lösung:

Analyse:

pr-10 

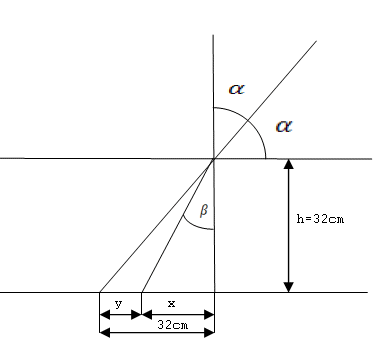
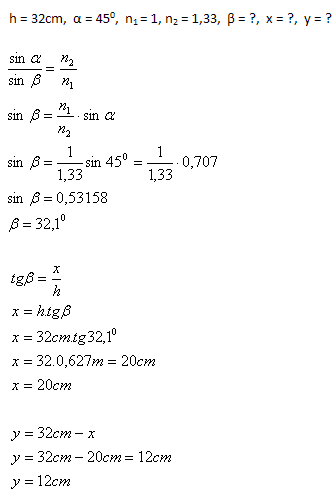
physics-reflection-and-refraction-10 

Der Stab berührt den Bachboden in einem Abstand von 12 cm vom Steinchen.