sk|cz|en|

Physik

Astrophysik

1.Wie werden in der Astrophysik Entfernungen, Massen und Helligkeiten von Sternen bestimmt?

Lösung:

 

Die Astrophysik untersucht die Struktur sowie die physikalischen und chemischen Eigenschaften von Himmelsobjekten – Sternen und Galaxien.

A. Entfernungseinheiten:

  • Astronomische Einheit (AU) als mittlere Entfernung von der Erde zur Sonne
    AU = 1,6 × 10¹¹ m

  • Das Lichtjahr (ly) ist die Strecke, die das Licht in einem Jahr zurücklegt
    ly = 9,46 × 10¹⁵ m = 63 241 AU

  • Ein Parsec ist die Entfernung, aus der 1 AU unter dem Winkel π = 1″ erscheint
    pc = 3,09 × 10¹⁶ m = 2,06 × 10⁵ AU = 3,261 ly

B. Masse von Sternen:

M=4π2K⋅r3T2K=6,67×10−11 kg−1m−3s−2M=\frac{4\pi^2}{K}\cdot\frac{r^3}{T^2} \qquad K=6{,}67\times10^{-11}\ \text{kg}^{-1}\text{m}^{-3}\text{s}^{-2}r13r23=2r12 (M1+m1)T22 (M1+m2)\frac{r_1^3}{r_2^3}=\frac{2r_1^2\,(M_1+m_1)}{T_2^2\,(M_1+m_2)}

r₁ = 1 AU, T₁ = 1 Jahr, (M₁ + M₁) = M☉, M₁ + m₁ ist in Einheiten der Erdmasse M☉

C. Sternhelligkeiten (Magnituden):

  • Scheinbare Magnitude (m): der Stern, wie er einem Beobachter auf der Erde erscheint

  • Absolute Magnitude (M): der Stern, wenn er aus der „Standard“-Entfernung beobachtet wird (Entfernung: 10 pc = 3,08568 × 10¹⁷ m)

m1−m1=M−5+5log⁡rm_1-m_1=M-5+5\log rm1−m2=−2,5log⁡Φ1Φ2m_1-m_2=-2{,}5\log\frac{\Phi_1}{\Phi_2}  

2.Wie werden Informationen über Sterne und das Universum gewonnen?

Charakterisieren Sie:

  • Wiensches Verschiebungsgesetz
  • Stefan–Boltzmann-Gesetz
  • Strahlungsfluss
  • Strahlungsleistung
  • Eigenschaften der Sonne
  • Expansion des Universums
  • Dopplersches Gesetz
  • Hubblesches Gesetz

Lösung:

 

Strahlung ist eine Informationsquelle über Sterne und das Universum.

Wiensches Verschiebungsgesetz:

λmax⁡=bT,b=2,88×102 mK,[λ]=m,[T]=K\lambda_{\max}=\frac{b}{T}, \qquad b=2{,}88\times10^{2}\ \text{m·K}, \qquad [\lambda]=\text{m}, \qquad [T]=\text{K}

Stefan–Boltzmann-Gesetz:

(Me=die Emissionsintensita¨t der Sternoberfla¨che)(M_e=\text{die Emissionsintensität der Sternoberfläche})Me=σT4,[L]=W,σ=5,67×10−3 Wm−2s3s−4,[T]=KM_e=\sigma T^{4}, \qquad [L]=\text{W}, \qquad \sigma=5{,}67\times10^{-3}\ \text{W·m}^{-2}\text{·s}^{3}\text{·s}^{-4}, \qquad [T]=\text{K}

Strahlungsfluss:

(Φ=Energie, die ein Stern pro Jahr abstrahlt)(\Phi=\text{Energie, die ein Stern pro Jahr abstrahlt})Φ=ΔΦΔt,Φ=Me s,[Φ]=W\Phi=\frac{\Delta\Phi}{\Delta t}, \qquad \Phi=M_e\,s, \qquad [\Phi]=\text{W}

Strahlungsleistung:

L=4nr2KSL=4nr^{2}\frac{K}{S}L=4nR3σT4,[L]=WL=4nR^{3}\sigma T^{4}, \qquad [L]=\text{W}

r = Entfernung des Sterns (Planeten) von S, R = Radius des Sterns (Planeten)
R₀ = 275 m·s⁻²
R = 1,5·10¹¹ m
m₀ = −26,8 m
L₀ = 3,83×10² W

Eigenschaften der Sonne:
M₀ = 1,99×10³² kg,    r = 1,5·10¹¹ m
R₀ = 6,96·10⁸ m, m₀ = −26,8 m
T₀ = 5780 K R₀ = 4,7 m
g₀ = 275 m·s⁻²,    L₀ = 3,83·10²⁶ W

Expansion des Universums:

Dopplersches Gesetz:

v=H⋅r,H=(77±25) kms−1Mpcv=H\cdot r, \qquad H=(77\pm25)\ \frac{\text{km·s}^{-1}}{\text{Mpc}}  

Hubblesches Gesetz:

v=H⋅r,H=(77±25) kms−1Mpc


3.Berechnen Sie, wie lange Licht im Vakuum benötigt, um eine Strecke zurückzulegen, die gleich ist mit

  • a) dem Durchmesser des Sonnensystems (s = 80 AE)
  • b) dem Durchmesser der Galaxie (s = 30 kpc)

Lösung:

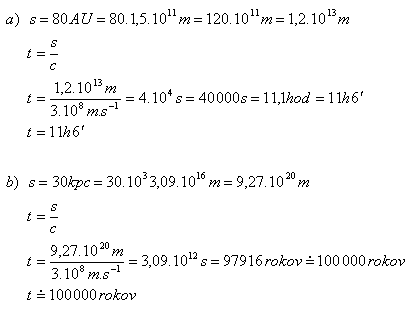
physics-astrophysics-3.gif

Licht durchquert den Durchmesser des Sonnensystems in 11 Stunden, den Durchmesser der Galaxie in etwa 100.000 Jahren.

4.Berechnen Sie die mittlere Materiedichte im Sonnensystem. Nehmen Sie an, dass die gesamte Masse des Systems in der Sonne liegt (Mo = 2·1030kg) und dass das Sonnensystem eine Kugel mit Radius R = 40 AE ist.

Lösung:

Analyse:

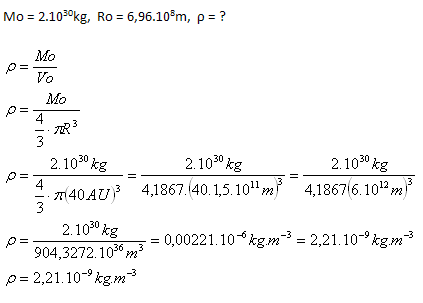
physics-astrophysics-4.gif

Die Materiedichte im Sonnensystem beträgt ρ = 2,21·10–9kg·m–3

5.Die Sonne umkreist das Zentrum der Galaxie mit v = 250 km·s-1, annähernd auf einer Kreisbahn mit Radius r = 10 kpc. Bestimmen Sie die Umlaufzeit der Sonne. Welche Gravitationskraft zieht die Sonne zum Zentrum der Galaxie?

Lösung:

Analyse:

physics-astrophysics-5.gif

  • Die Umlaufzeit der Sonne um das Zentrum der Galaxie beträgt etwa 250 Millionen Jahre.
  • Die Sonne wird zum Zentrum der Galaxie durch eine Gravitationskraft Fg = 4·1020N angezogen.

6.Betrachten Sie einen Kugelsternhaufen mit Masse MGC = 2·105Mo, der das Zentrum der Galaxie (MG = 1,4·1011Mo) auf einer Kreisbahn mit Radius r = 12 kpc umkreist. Bestimmen Sie:

  • a) die Kraft, mit der der Haufen zum Zentrum der Galaxie hingezogen wird
  • b) die Zentripetalbeschleunigung des Haufens
  • c) die Geschwindigkeit des Haufens relativ zum Zentrum der Galaxie

Lösung:

Analyse:

physics-astrophysics-6.gif

  • Die Kraft, die den Haufen zum Zentrum der Galaxie anzieht, beträgt Fg = 5,4·1025N
  • Die Zentripetalbeschleunigung des Haufens beträgt a = 1,4·10–10m·s-2
  • Die Geschwindigkeit des Haufens relativ zum Zentrum der Galaxie beträgt v = 228 km·s-1

7.Leiten Sie die Formel zur Berechnung der Masse eines Sterns (Planeten) mithilfe seines Satelliten her.

Lösung:

Analyse:

M = Masse des Sterns, m = Masse des Satelliten, r = Radius der kreisförmigen Umlaufbahn des Satelliten, T = Umlaufzeit des Satelliten, κ = 6,67·10–11N·m2·kg-2

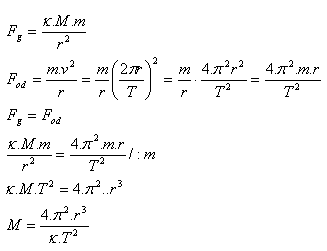
physics-astrophysics-7-1.gif

Die Masse des Sterns wird berechnet nach:

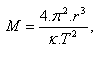
physics-astrophysics-7-2.gif

8.Berechnen Sie die Masse des Planeten Mars mithilfe seines Mondes Deimos, der Mars auf einer Kreisbahn mit Radius r = 23,5·106m und einer Umlaufzeit von 1,26 Erdtagen umkreist.

Lösung:

Analyse:

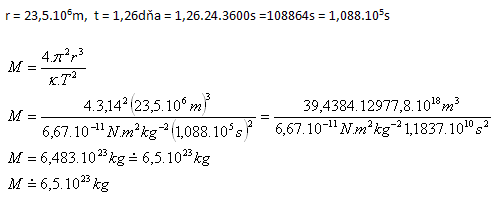
physics-astrophysics-8.gif

Die Masse des Mars beträgt M = 6,5·1023kg.

9.Jupiters Mond Europa umkreist Jupiter auf einer Kreisbahn mit Radius r1 = 6,71·108m und Umlaufzeit T = 3,88 Tage. Berechnen Sie, um wie vielmal die Masse des Jupiter größer ist als die Masse der Erde.

Lösung:

Jupiter + Europa: M1 + m1, r1 = 6,71·108m, T1 = 3,88 Tage,
Erde + Mond: M2 + m2, r2 = 3,844·108m = 1 Monat = 30 Tage
m1 – vernachlässigbar, m2 – vernachlässigbar gegenüber M1 und M2

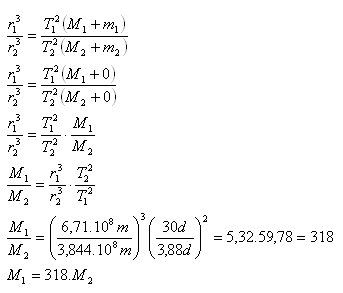
physics-astrophysics-9.gif

Die Masse des Jupiter ist 318-mal größer als die der Erde.

10.Die Gesamtmasse eines Doppelsterns beträgt 3,5Mo; die Komponenten umkreisen ihren gemeinsamen Schwerpunkt mit der Periode T = 320 Jahre. Bestimmen Sie die gegenseitige Lage der Komponenten senkrecht zur Sichtlinie, die wir unter einem Winkel π = 3,1″ sehen würden, sowie die Entfernung des Doppelsterns von der Sonne.

Lösung:

Analyse:

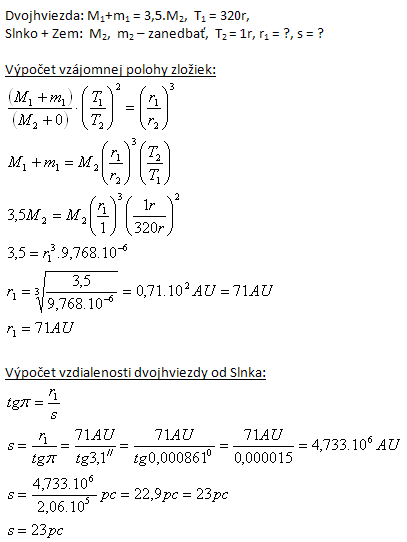
physics-astrophysics-10.gif

11.Die scheinbare Sternhelligkeit (scheinbare Magnitude) der Sonne beträgt -26,8m. Berechnen Sie ihre absolute Magnitude M.

Lösung:

Analyse:

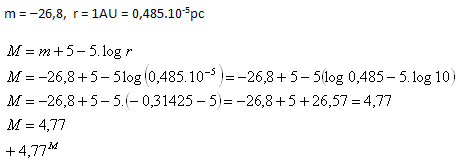
physics-astrophysics-11.gif

Die absolute Sternhelligkeit der Sonne beträgt +4,77M.

12.Bis zu welcher Entfernung können wir mit einer Supernova Galaxienentfernungen messen, wenn ihre maximale absolute Magnitude –16M beträgt und wir ein Teleskop haben, das Sterne bis zur scheinbaren Magnitude +22m beobachtet?

Lösung:

Analyse:

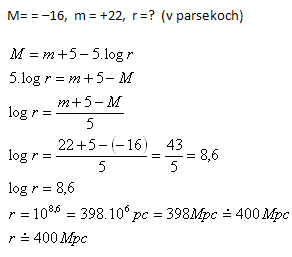
physics-astrophysics-12.gif

Das Teleskop kann bis zu einer Entfernung von etwa 400 Mpc genutzt werden.

13.Welche Parallaxe π hat ein Stern, wenn die Differenz zwischen seiner scheinbaren und absoluten Magnitude +8 beträgt?

Lösung:

Analyse:

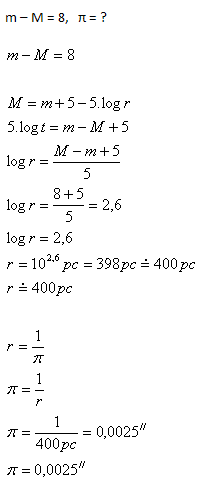
physics-astrophysics-13.gif

Der Stern hat eine Parallaxe π = 0,0025″.

14.Welche Wellenlänge hat die maximale Strahlung und wie groß ist die Strahlungsintensität eines Sterns mit einer Temperatur von 30.000K?

Lösung:

Analyse:

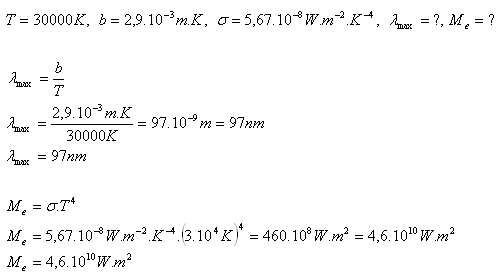
physics-astrophysics-14.gif

Die Wellenlänge beträgt λ = 97nm, die Strahlungsintensität des Sterns ist Me = 4,6·1010W·m2.

15.Ein Roter Riese hat eine Oberflächentemperatur von 3500K, Radius R = 36Ro, Masse M = 3,6Mo. Berechnen Sie seine mittlere Dichte ρ und die Strahlungsleistung L. (σ = 5,67·10-8W·m-2·K–4)

Lösung:

Analyse:

physics-astrophysics-15.gif

Die mittlere Dichte des Roten Riesen beträgt ρ = 0,11 kg·m-3 und seine Strahlungsleistung L = 671·1028W.

16.Berechnen Sie den Radius und die mittlere Dichte eines Weißen Zwergs mit Masse M = 2,35Mo, Oberflächentemperatur T = 12.500K, Strahlungsleistung L = 0,0036Lo. Ro = 6,96·108m, T0 = 5780K

Lösung:

Analyse:

physics-astrophysics-16.gif

Der Radius des Weißen Zwergs beträgt R = 9·106m und seine mittlere Dichte ρ = 2,28·108kg·m–3.

17.Welche Strahlungsleistung (Strahlungsfluss) der Sonne fällt auf eine Fläche S = 1m2 (Strahlungsleistung der Sonne L = 3,83·1026W)

  • auf der Venus (r = 0,72 AE)
  • auf dem Jupiter (r = 5,2 AE)

Lösung:

Analyse:

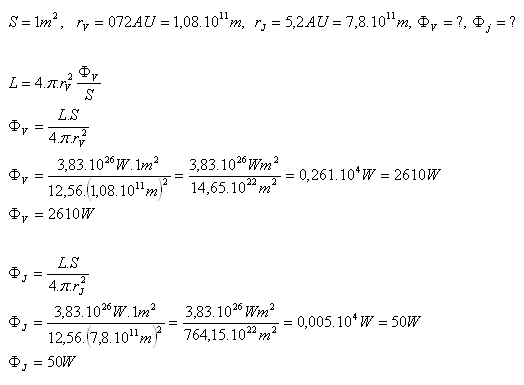
physics-astrophysics-17.gif

  • Der Strahlungsfluss auf 1m2 der Venus beträgt ФV = 2610W,
  • auf 1m2 des Jupiter beträgt ФJ = 50W.

18.Ein Stern hat eine scheinbare Magnitude m1 = 4. Welche scheinbare Magnitude m2 hätte er, wenn er in doppelter Entfernung wäre?

Lösung:

Analyse:

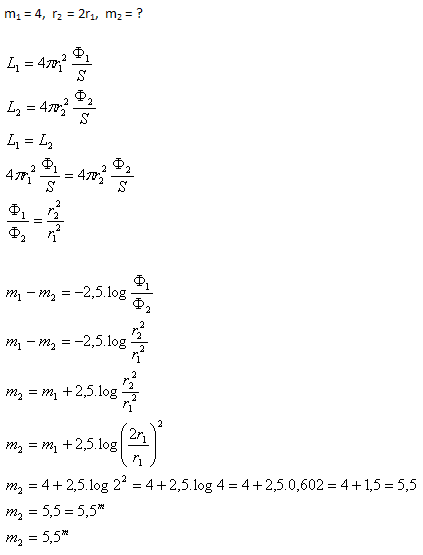
physics-astrophysics-18.gif

In doppelter Entfernung wäre die scheinbare Magnitude des Sterns 5,5m.

19.Betrachten Sie eine ferne Galaxie, die sich mit einer Geschwindigkeit v = 6000 km·s-1 von unserer Galaxie entfernt. Welche Wellenlänge der Wasserstoff-Spektrallinie werden wir messen, wenn ihre ursprüngliche Wellenlänge 656,3 nm beträgt? In welcher Entfernung von uns befindet sich diese Galaxie wahrscheinlich?

Lösung:

Analyse:

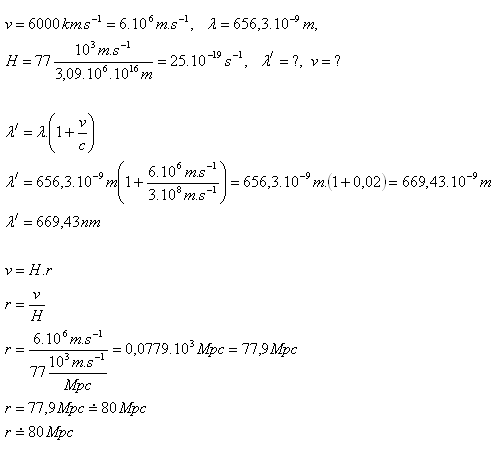
physics-astrophysics-19.gif 

Die Wellenlänge erhöht sich auf einen Wert von λ' = 669,43 nm. Die Galaxie ist etwa 80 Mpc von uns entfernt.

20.Bestimmen Sie die Zeitspanne, über die sich unser Universum ausdehnt. Bestimmen Sie die Zeit, die seit dem „Urknall“ bis heute vergangen ist.

Lösung:

Analyse:

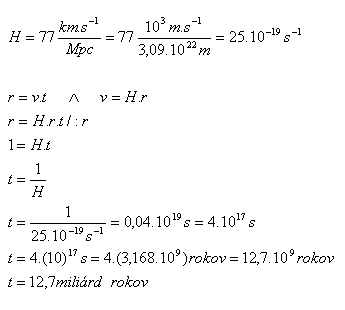
physics-astrophysics-20.gif 

Seit dem „Urknall“ sind etwa 13 Milliarden Jahre vergangen. Die Berechnung hängt von der Wahl der Hubble-Konstante H ab.

Für H gilt: 16,13·10–19s-1 < 25·10-19s-1 < 32,26·10–19s-1.