Radioaktivität

1. Was ist Radioaktivität?

Lösung:

Radioaktivität ist die Umwandlung (der Zerfall) von Atomkernen. Der Kern eines Elements wandelt sich allmählich in den stabilen Kern eines anderen Elements um, wobei Energie freigesetzt wird. Natürliche Radioaktivität (M. Becquerel und P. Curie) ist der spontane Zerfall instabiler Kerne. Künstliche Radioaktivität (I. und F. Joliot Curie) entsteht durch künstlich herbeigeführte Kernreaktionen.

Natürliche Radioaktivität

Verschiebungsregeln:

Alphazerfall:

{}^{A}_{Z}X \rightarrow {}^{A-4}_{Z-2}Y + \alpha

Beta-Plus-Zerfall (β⁺):

{}^{A}_{Z}X \rightarrow {}^{A}_{Z-1}Y + \nu

Beta-Minus-Zerfall (β⁻):

{}^{A}_{Z}X \rightarrow {}^{A}_{Z+1}Y + \bar{\nu}

Gammazerfall (γ):

{}^{A}_{Z}X \rightarrow {}^{A}_{Z}X^{*} + \gamma

$_{0}^{- 1} e$ = Elektron,
${}^{0}_{+1}e$ = Positron,
$\nu$ = Neutrino,
$\bar{\n$ = Antineutrino

Gesetz des radioaktiven Zerfalls:

$N_t$ = Anzahl der nicht zerfallenen Kerne

N_t = N_0 e^{-\lambda t}, \qquad \lambda = \frac{\ln 2}{T}

$T$ = Halbwertszeit — die Zeit, nach der genau die Hälfte der Kerne zerfallen ist.

Gesetz der radioaktiven Umwandlung:

$N'_t$ = Anzahl der zerfallenen Kerne

N'_t = m \frac{N_A}{M} \left(1 - e^{-\lambda t}\right), \qquad \text{or approximately:} \qquad N'_t = \frac{m}{A\,u} \frac{\ln 2}{T} \, t

2.Bestimmen Sie die Abfolge der radioaktiven Umwandlungen in der Thorium-Zerfallsreihe.

Lösung:

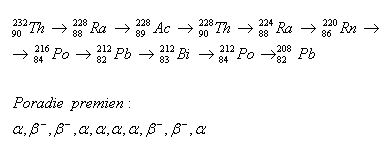
Reihenfolge der Umwandlungen:

3. Bestimmen Sie die Zusammensetzung des Atomkerns des Isotops des Elements, das aus Uran entsteht.

Lösung:

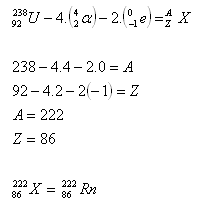
Das gesuchte Element ist ein Isotop von Radon. [Bestimmt mithilfe von Tabellen].

4.Vervollständigen Sie die Kernreaktionsgleichungen:

Lösung:

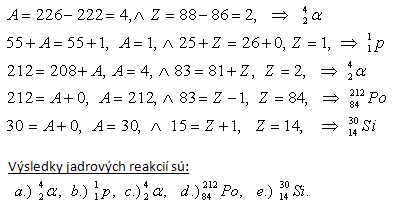
Die Ergebnisse der Kernreaktionen sind:

5.Bestimmen Sie die Halbwertszeit von Uran, wenn seine Zerfallskonstante λ = 4.33·10^-4 Jahr^-1 ist.

Lösung:

Analyse:

λ = 4.33·10^-4 Jahr^-1

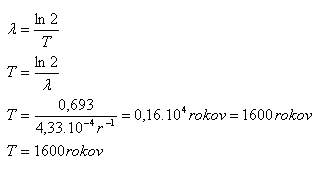
Nach 1600 Jahren ist genau die Hälfte der Urankerne zerfallen.

6.Ein Nuklid hat eine Halbwertszeit von 2400 Sekunden. Welcher Prozentsatz der Kerne zerfällt in 300 Sekunden?

Lösung:

Analyse:

T = 2400s, t = 300s, ln2 = 0.693, e = 2.718282, N = ?, N‘ = ?

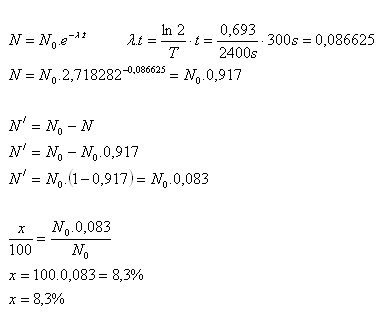
In 300 Sekunden zerfallen 8.3% der Kerne.

7.Die Anzahl der Zerfälle in 1 Gramm Radium beträgt 3.7·10¹⁰s^-1. Bestimmen Sie die Halbwertszeit.

Lösung:

Analyse:

m = 1g = 10^–3kg, N‘ = 3.7·10¹⁰s^-1, A = 226, m_u = 1.6605·10^–27kg, T = ?, 1 Jahr = 3.15·10⁷s

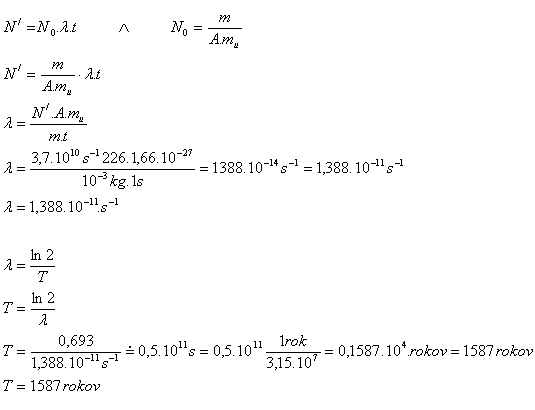
Die Halbwertszeit von Radium beträgt etwa 1587 Jahre.

8.Nach welcher Zeit wird die Hälfte der Kerne eines Radionuklids zerfallen sein, wenn seine Zerfallskonstante λ = 1.42·10^–11s^-1 ist?

Lösung:

Analyse:

λ = 1.42·10^–11s^-1, 1 Jahr = 3.1536·10⁷s, ln e = 1, ln 0.5 = –0.693, t = ?

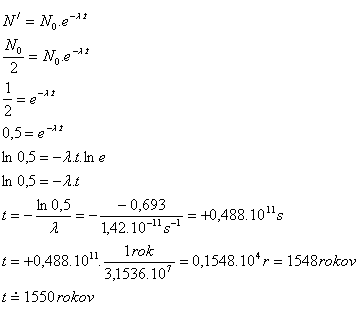
Die Hälfte der Radionuklidkerne wird in etwa 1550 Jahren zerfallen sein.

9.Bei der Bestimmung des Alters des Begräbnisbootes aus dem Grab von Sesostris III wurde festgestellt, dass die Kohlenstoffkonzentration im Holz, aus dem das Boot gefertigt wurde, ungefähr N = 0.645·N₀ beträgt. N₀ ist die Kohlenstoffkonzentration in heutigen lebenden Organismen. Bestimmen Sie das Alter des Begräbnisbootes, wenn die Halbwertszeit von Kohlenstoff 5730 Jahre beträgt.

Lösung:

Analyse:

N = 0.645·N₀, T = 5730 Jahre, ln2 = 0.693, t = ?

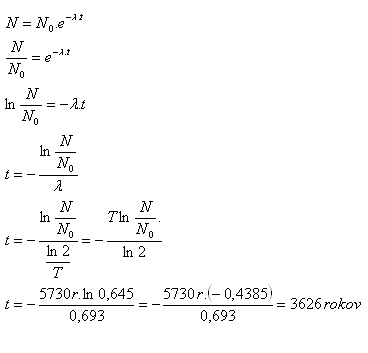
Sesostris III wurde vor 3626 Jahren beigesetzt.

Zur Bestimmung des Alters archäologischer Objekte wurde die sogenannte „Kohlenstoffmethode“ verwendet.

10.Im September 1991 entdeckten Touristen in den Ötztaler Alpen in Österreich einen eis-mumifizierten menschlichen Körper. Mit der Kohlenstoffmethode wurde festgestellt, dass für die nicht zerfallenen Kerne in seinem Körper N und die Kerne in den Körpern heutiger Menschen N gilt: N = 0.5268·N₀. Wie viele Jahre ist es her, dass dieser Mann erfror, wenn die Halbwertszeit von Kohlenstoff T = 5730 Jahre beträgt?

Lösung:

Analyse:

N = 0.5268·N₀, T = 5730 Jahre, ln2 = 0.693

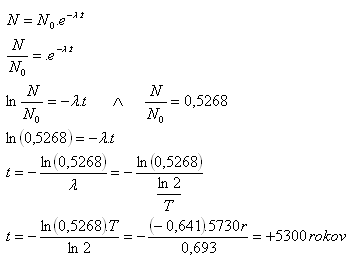
Der Mann in den Alpen erfror vor etwa 5300 Jahren.

11.Die Halbwertszeit des Nuklids Radium beträgt 1622 Jahre. Bestimmen Sie seine Zerfallskonstante λ.

Lösung:

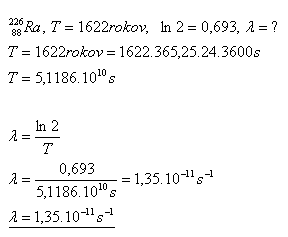
radioaktivita-11

Die Zerfallskonstante des Radium-Nuklids beträgt λ = 1.35·10^–11s^–1.

12.Radium hat eine Halbwertszeit T = 1622 Jahre. Nach welcher Zeit wird die Anzahl der Radiumkerne auf 0.1% der ursprünglichen Anzahl sinken?

Lösung:

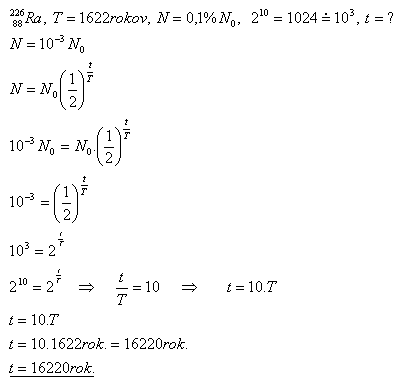
radioaktivita-12

Die Anzahl der Radiumkerne wird nach 16,220 Jahren auf 0.1% der ursprünglichen Menge sinken.

13.Derzeit hat 1 g Radium 2.68·10²¹ Kerne. Wie viele

a.) nicht zerfallene Kerne
b.) zerfallene Kerne nach 4000 Jahren?

Lösung:

radioaktivita-13

Es wird 0.4853·10²¹ nicht zerfallene Kerne und 2.195·10²¹ zerfallene Kerne geben.

14.Während einer Zeit von 49.2 Stunden sinkt die Aktivität von radioaktivem Natrium auf 0.1 ihres Anfangswertes. Wie groß ist die Halbwertszeit dieses Nuklids?

Lösung:

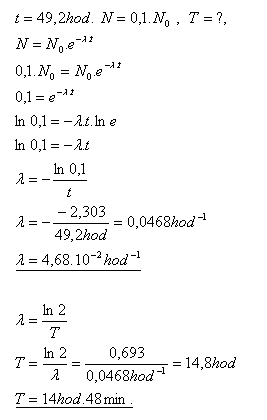
radioaktivita-14

Die Halbwertszeit des Natrium-Nuklids beträgt 14 h 48 min.

15.Der Kern von Uran (Z = 92, A = 238) zerfällt nacheinander in andere Kerne. In dieser Zerfallskette treten 8 α-Zerfälle und 6 β^–-Zerfälle auf. Was ist das Endprodukt dieser Zerfallsreihe?

Lösung:

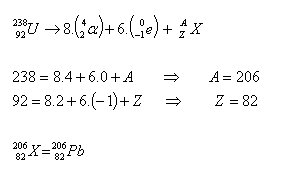
radioaktivita-15

Das Endprodukt dieses Zerfalls ist Blei ²⁰⁶₈₂Pb.

16.In einer Kettenreaktion löst ein Neutron, das auf den Kern ²³⁵₉₂U trifft, die Spaltung des Kerns in zwei mittelschwere Kerne aus und setzt außerdem mehrere Neutronen frei. Wie viele Neutronen werden in der folgenden Reaktion freigesetzt?

Lösung:

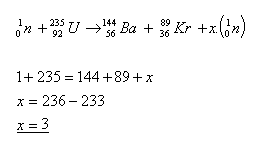
radioaktivita-16

In der Kettenreaktion werden 3 Neutronen freigesetzt.

17.Zeigen Sie, dass wir, wenn λt << 1 gilt, die Beziehung N^/ = N₀·λ·t zur Berechnung der Anzahl der zerfallenen Kerne verwenden können.

Lösung:

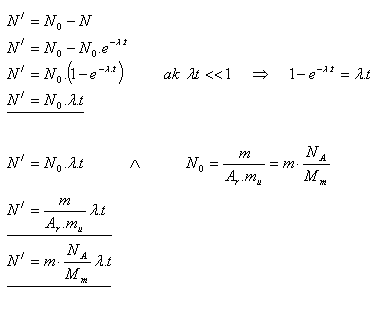
radioaktivita-17

18.Eine dünne Folie, die 1 Gramm des Nuklids Thorium ²³²₉₀Th enthält, emittiert 4100 α-Teilchen pro Sekunde. Bestimmen Sie die Halbwertszeit dieses Nuklids.

Lösung:

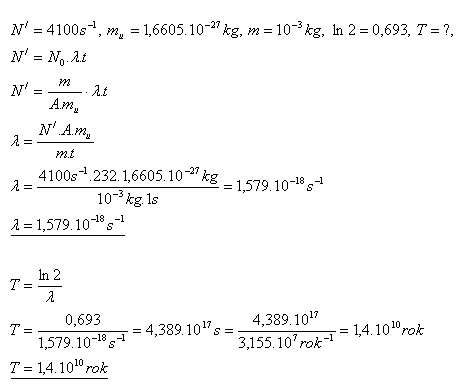
radioaktivita-18

Die Halbwertszeit des Nuklids Thorium ²³²₉₀Th beträgt T = 1.4·10¹⁰ Jahre.

19.Welcher Prozentsatz der ursprünglichen Menge eines radioaktiven Elements zerfällt während einer Zeit, die seiner mittleren Lebensdauer entspricht?

Lösung:

radioaktivita-19

Während der mittleren Lebensdauer zerfallen 63% der ursprünglichen Menge des radioaktiven Elements.

20.Anfang des 20. Jahrhunderts entdeckten bedeutende Physiker in Experimenten, dass ein stabiler Atomkern durch einen äußeren Einfluss gespalten werden kann. Dies führte zur Entdeckung der künstlichen Radioaktivität. Es gelang ihnen, Stickstoff in ein Isotop von Sauerstoff umzuwandeln, Beryllium in Kohlenstoff, und sie fanden eine Methode, Aluminium in Phosphor und dann in Silizium umzuwandeln. In jedem dieser Experimente wurde ein neues Elementarteilchen entdeckt.

WELCHES?

Lösung:

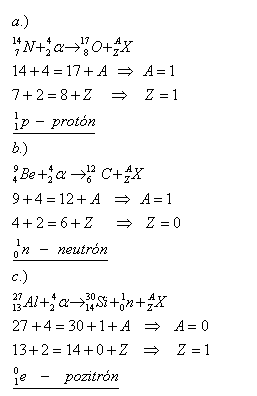
radioaktivita-20

E. Rutherford entdeckte 1919 das Proton, J. Chadwick entdeckte 1932 das Neutron, und C. Anderson entdeckte 1932 das Positron.

Physik

Radioaktivität

Adblock detected