Atomverpackung
1. Wie sieht ein Atom aus?
Lösung:
Aristoteles (384 v. Chr.): Materie ist kontinuierlich und kann unendlich geteilt werden. Leukipp, Demokrit (5. Jh. v. Chr.): Materie ist diskontinuierlich und besteht aus unteilbaren Teilchen – Atomen. J. J. Thomson (1856–1940) entwickelte das sogenannte „Rosinenkuchenmodell“. Das Atom ist eine positiv geladene Kugel, in der Elektronen eingebettet sind. E. Rutherford (1871–1937) entwickelte das „planetarische Atommodell“. Die gesamte Masse des Atoms (sowie seine positive Ladung) ist im Kern (10–15 m) konzentriert. Um den Kern kreisen die Elektronen auf Kreisbahnen (Ellipsen – A. Sommerfeld). Der Radius des Atoms beträgt etwa 10–10 m. Der Hauptnachteil dieses Modells war, dass das Elektron beim Umlauf um den Kern Energie verlieren müsste, seine Geschwindigkeit abnähme, es spiralartig in den Kern stürzen würde und damit die materielle Welt nicht existieren könnte. N. Bohr (1883–1962) entwickelte das „quantentheoretische Atommodell“.
- a.) Ein Elektron kann sich um den Kern nur auf bestimmten Kreisbahnen bewegen, die Orbitale (Energieniveaus) genannt werden. Die Länge eines Orbitals ist gleich einem ganzzahligen Vielfachen der Wellenlänge der dem Elektron entsprechenden de-Broglie-Welle.
- b.) Bewegt sich das Elektron auf einem Orbital, so sendet es keine Energie aus.
- c.) Beim Übergang des Elektrons von einem Orbital mit der Energie En zu einem Orbital mit geringerer Energie Em wird ein Lichtquant – ein Photon – emittiert. K. Heisenberg (1901–1976), E. Schrödinger (1887–1961) entwickelten das „quantenmechanische, probabilistische Modell“. Es ist nicht möglich, Ort und Geschwindigkeit eines Elektrons gleichzeitig mit gleicher Genauigkeit zu bestimmen. Man kann nur Bereiche angeben, in denen sich das Elektron mit einer bestimmten Wahrscheinlichkeit um den Kern aufhält.
2. Welche Eigenschaften hat das Wasserstoffatom im Bohrschen Modell?
Lösung:
Bedingung für den Radius eines Orbitals:
2πr = (n h) / (mₑ v) n = 1, 2, 3, 4, … — Hauptquantenzahl,
h = 6.625·10⁻³⁴ J·s, mₑ = 9.1·10⁻³¹ kg
Energie des emittierten Quants, wenn ein Elektron zwischen zwei Orbitalen springt:
h f = Eₙ − Eₘ Eₙ > Eₘ
Die niedrigste Energie hat das Elektron auf der Bahn, die dem Kern am nächsten ist.
E₁ = −13.6 eV
Eₙ = E₁ / n²
Geschwindigkeit des Elektrons, das sich auf einem Orbital bewegt:
v₁ = 2.18·10⁶ m·s⁻¹
vₙ = v₁ / n
vₙ = (2π k e²) / (h n) k = 9·10⁹ N·m²·C⁻², e = 1.602·10⁻¹⁹ C
Rydbergsches Gesetz:
f = R (1/m² − 1/n²) R = 3.29·10¹⁵ Hz
3. Wie lange benötigt Licht, um ein Atom mit dem Radius r = 3.10–10 m zu durchqueren?
Lösung:
Analyse:
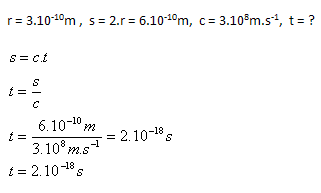
Licht durchquert das Atom in t = 2.10–18 s.
4. Berechnen Sie die Energie des Grundzustands des Wasserstoffatoms E1. 1 J = 0.6242.1019 eV
Lösung:

Die Energie des Grundzustands des Wasserstoffatoms beträgt E1 = –13,6 eV.
5. Berechnen Sie die Energien des Wasserstoffatoms auf stationären Bahnen mit der Hauptquantenzahl n = 1,2,3,4,5,6. Die Energie der ersten Bahn ist E1 = –13,6 eV. (Beispiel 4)
Lösung:
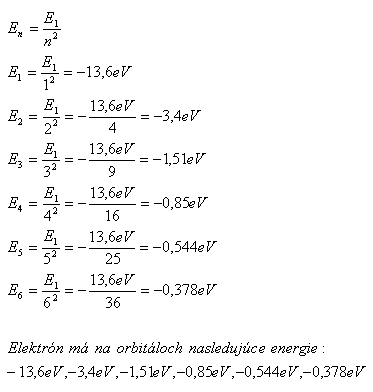
Ein Elektron besitzt in seinen Orbitalen folgende Energie
6. Berechnen Sie die Geschwindigkeiten des Elektrons auf den einzelnen Orbitalen im Wasserstoffatom, wobei gilt:
r1 = 0,53.10–10 m.
Lösung:
Analyse:
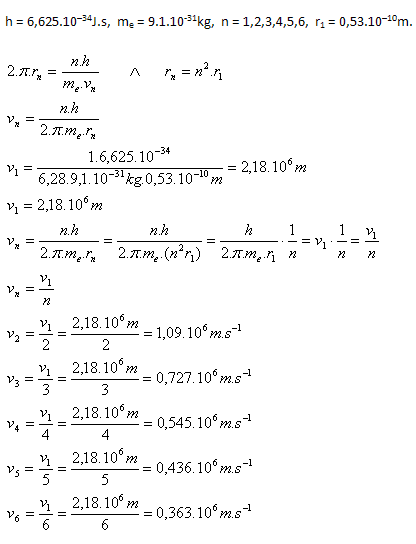
7. Bestimmen Sie die Frequenzen der sichtbaren Linien der Balmer-Serie (J. Balmer, 1825–1898) für Wasserstoff. Die Serie entsteht durch Elektronenübergänge auf die zweite Bahn.
Lösung:
Analyse:
E1 = –13,6 eV, E2 = –3,4 eV, E3 = –1,5 eV,
E4 = –0,85 eV, E5 = –0,544 eV, E6 = –0,378 eV
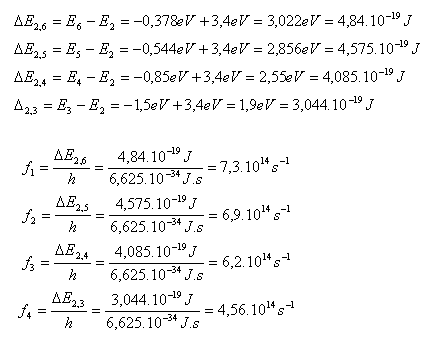
8. Ein Wasserstoffatom im Grundzustand absorbiert eine Energie von 10,2 eV. Auf welches Energieniveau geht das Elektron über?
Lösung:
Analyse:
ΔE = 10,2 eV, E1 = –13,6 eV, n = ?
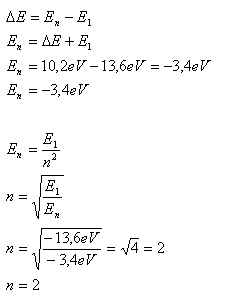
Das Elektron ist auf das zweite Energieniveau übergegangen.
9. Ein Helium-Neon-Laser hat eine Leistung von 2 mW und sendet Strahlung mit der Wellenlänge 632,8 nm aus. Bestimmen Sie die Energie, Masse und den Impuls der emittierten Photonen.
Lösung:
Analyse:
P = 2.10–3 W, λ = 632,8.10–9 m, E = ?, m = ?, p = ?
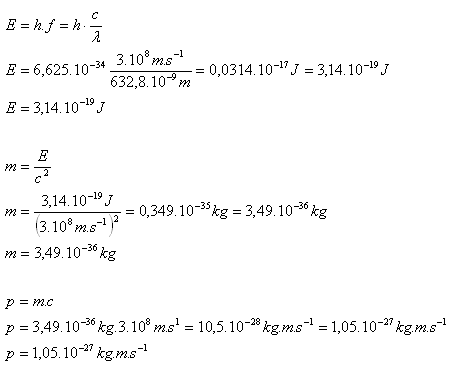
Ein Photon besitzt die Energie E = 3,14.10–18 J, die Masse m = 3,49.10–36 kg und den Impuls p = 1,05.10–27 kg·m·s–1.
10. Das Wasserstoffatom geht vom stationären Zustand n = 6 in den Zustand m = 1 über. Berechnen Sie die Frequenz und die Wellenlänge des emittierten Photons. Verwenden Sie die Rydberg-Formel. (J. R. Rydberg 1854–1919)
Lösung:
Analyse:
n = 6, m = 1, R = 3,29.1015 s–1
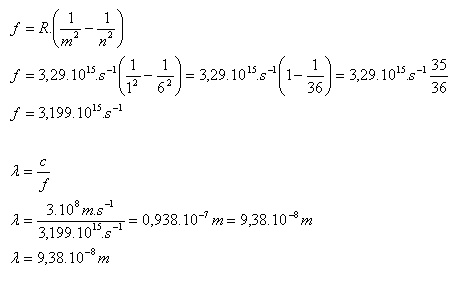
Das emittierte Photon besitzt die Frequenz f = 3,199.1015 Hz und die Wellenlänge λ = 9,38.10–8 m.
11. Berechnen Sie die Menge der elektromagnetischen Energie, die von einem Wasserstoffatom emittiert wird, wenn sein Elektron von der ersten Bahn auf eine unendlich weit entfernte Bahn springt.
Lösung:
Analyse:
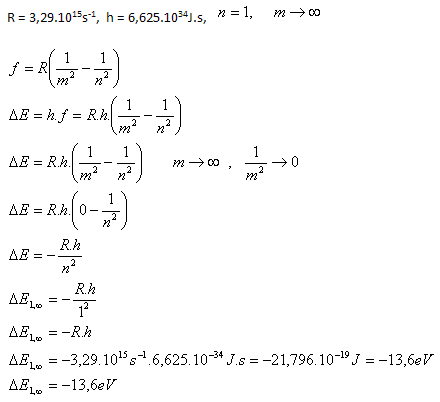
Das Wasserstoffatom emittiert –13,6 eV elektromagnetischer Energie.
12. Leiten Sie die Rydberg-Konstante R her
Lösung:
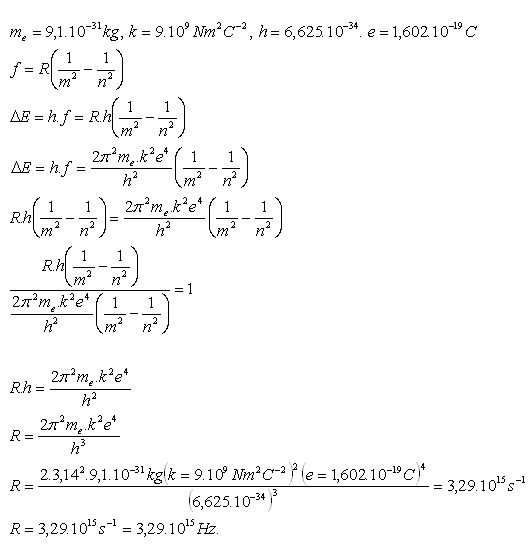
13. Bestimmen Sie die drei längsten Wellenlängen der Balmer-Serie. Diese Serie entspricht der Emission von Energie durch ein Elektron bei den Übergängen 3 → 2, 4 → 2, 5 → 2.
Lösung:

Die längsten Wellenlängen der Balmer-Serie entsprechen den Farben Rot, Blau und Violett.
14. Welche Spannung muss in einem elektrischen Feld anliegen, wenn wir ein Elektron so beschleunigen wollen, dass es bei einer Kollision mit einem Wasserstoffatom das Atom vom Grundzustand in den ersten angeregten Zustand anregen kann?
Lösung:
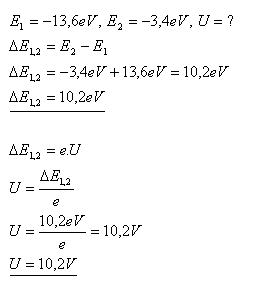
Die Spannung im elektrischen Feld muss U = 10,2 V betragen.
15. Der Radius der ersten Kreisbahn des Elektrons im Wasserstoffatom beträgt r = 0,53×10–10 m. Bestimmen Sie die Stärke des elektrischen Feldes des Kerns auf dieser Bahn.
Lösung:
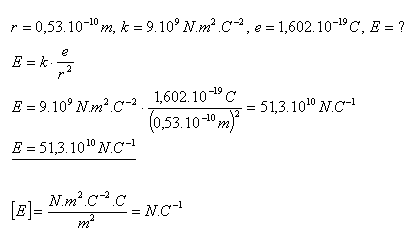
Die elektrische Feldstärke auf der ersten Bahn des Elektrons im Wasserstoffatom beträgt E = 51,3×1010 N·C–1.
16. Welches Potenzial hat der Atomkern auf der ersten Elektronenbahn im Wasserstoffatom?
(E = 51,3×1010 N·C–1 – Beispiel 15)
Lösung:
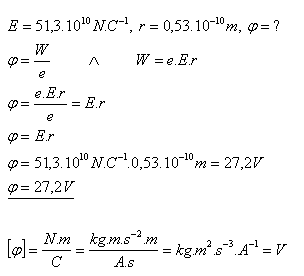
Das Potenzial auf der ersten Elektronenbahn im Wasserstoffatom beträgt φ = 27,2 V.
17. Bestimmen Sie, ob der photoelektrische Effekt auftreten kann, wenn sichtbares Licht auf Zink fällt. WV(Zn) = 4 eV. Die kürzeste Wellenlänge des sichtbaren Lichts ist λ = 390 nm.
Lösung:
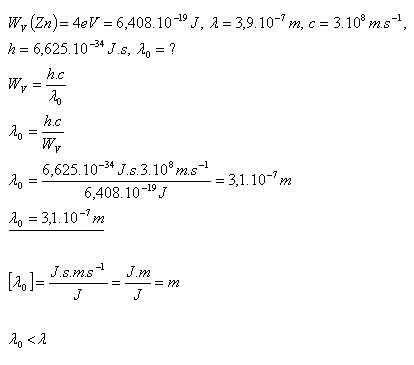
Photoemission tritt nicht auf, da λ0 < λ.
18. Die Austrittsarbeit von Platin beträgt WV(Pt) = 5,29 eV. Berechnen Sie die Grenzfrequenz f0, bei der der photoelektrische Effekt auftritt.
Lösung:
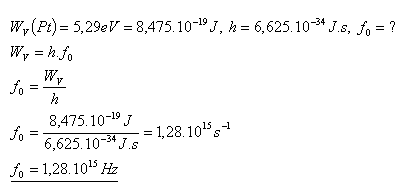
Die Grenzfrequenz beträgt f0 = 1,28×1015 Hz.
19. Wie groß ist die Geschwindigkeit der Elektronen, die aus der Oberfläche von Cäsium emittiert werden, wenn es mit monochromatischem Licht der Wellenlänge λ = 590 nm bestrahlt wird? Die Austrittsarbeit von Cäsium beträgt WV(Cs) = 1,93 eV.
Lösung:
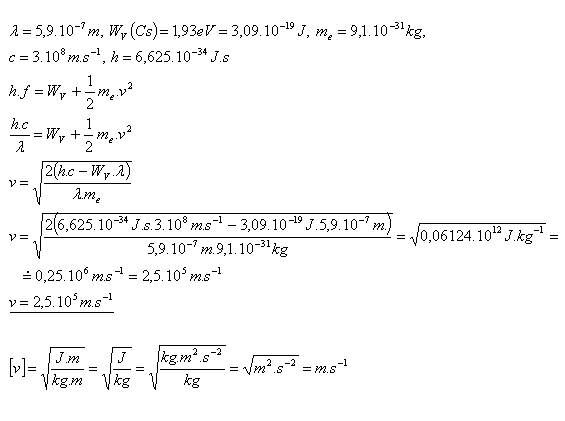
Die Elektronen verlassen die Oberfläche von Cäsium mit der Geschwindigkeit v = 2,5×105 m·s–1.
20. Leiten Sie die Beziehung zur Berechnung der Energie eines Elektrons her, das in einem Segment der Länge L eingeschlossen ist.
Lösung:
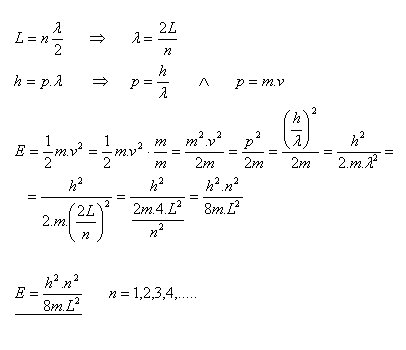
21. Welche Energie haben der Grundzustand und der erste angeregte Zustand eines Elektrons, das in einem Segment der Länge L = 4×10–10 m eingeschlossen ist?
Lösung:
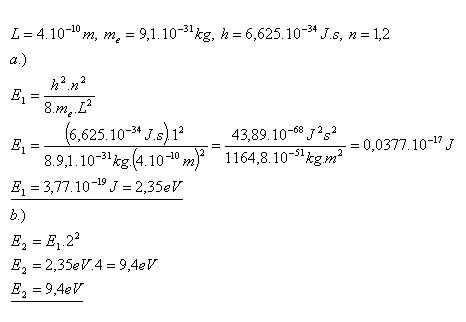
Die Energien des Elektrons sind E1 = 2,35 eV, E2 = 9,4 eV.
22. Wie groß muss die Länge des Segments sein, in dem ein Elektron eingeschlossen ist, damit der Unterschied zwischen Grundzustand und erstem angeregten Zustand kleiner als 3 eV ist?
Lösung:
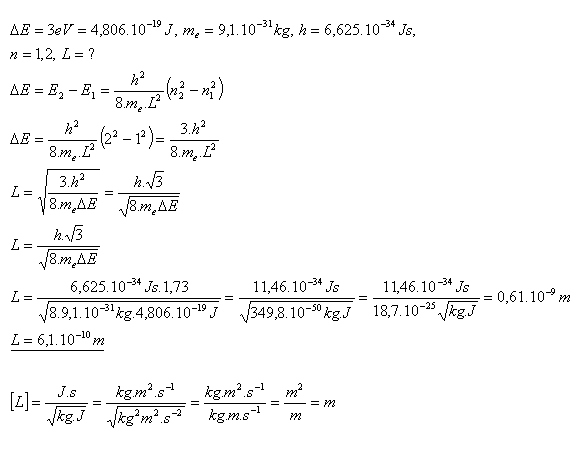
Die Länge des Segments muss etwa L = 6×10–10 m betragen.
23. Wie lautet die Elektronenkonfiguration von Natrium, Eisen, Kupfer und Silber? Verwenden Sie die Tabelle aus Beispiel Nr. 2.
Lösung:
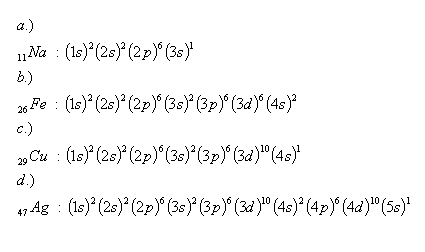
24. Welche Elemente besitzen die folgenden Konfigurationen:
Lösung:
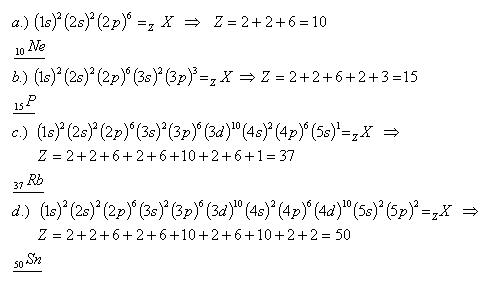
Es handelt sich um die Elemente Neon, Phosphor, Rubidium und Zinn.
25. Bestimmen Sie die Energie des Elektrons im Grundzustand des Butadien-Moleküls mit der Konfiguration (1s)2(2s)2. Die Elektronen bewegen sich entlang der gesamten Moleküllänge L = 0,6×10–9 m.
Lösung:
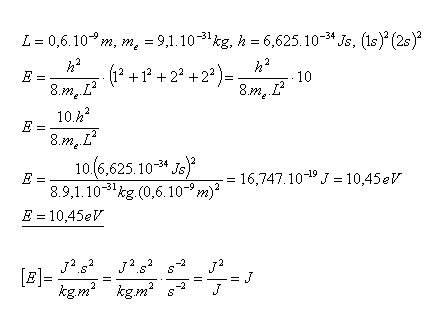
Die Energie des Elektrons im Grundzustand des Butadien-Moleküls beträgt E = 10,45 eV.